How can I modify this python code to produce a 2-start globoid worm gear in Blender?

Question

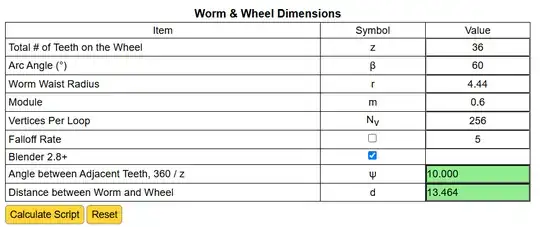
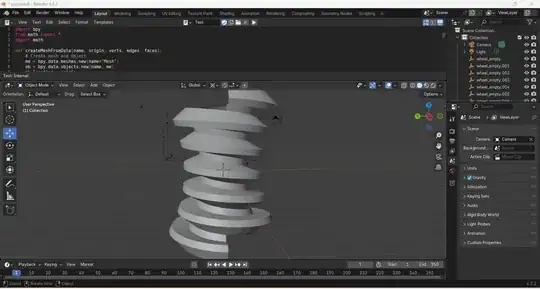
I am designing a device that uses a double-throated, globoid worm. I am using a gear generator program to produce the worm in Blender. Using inputs given by the user, the gear generator provides a python code that I then paste into the Scripting Text Editor window in Blender. Blender then produces the resulting globoid worm from those inputs. However, the program does not have any inputs to create a 2-start gear, only a 1-start gear. Can someone help me modify the code so that it produces the modified gear?

Here is the Gear Generator I'm using: https://www.otvinta.com/instantworm.html

Here are my inputs:

Here is the code that it provides:

import bpy
from math import *
import math
def createMeshFromData(name, origin, verts, edges, faces):
    # Create mesh and object
    me = bpy.data.meshes.new(name+'Mesh')
    ob = bpy.data.objects.new(name, me)
    ob.location = origin
    ob.show_name = False
    # Link object to scene and make active
    bpy.context.collection.objects.link(ob)
    ob.select_set(True)
# Create mesh from given verts, faces.
me.from_pydata(verts, edges, faces)
# Update mesh with new data
me.update()


def HandleFalloff( r, u, MaxRadius, Falloff ):
    if Falloff == 0:
        return r
    else:
        return r + (MaxRadius - r) * 6 * (pow(u, Falloff * 4) / 2 - pow(u, Falloff * 6) / 3)
def XFunc(R, r, u, AK, Delta, TB, Falloff, MaxRadius):
    r = HandleFalloff( r, u, MaxRadius, Falloff )
    return - (R - r * math.cos(u * math.pi / AK + Delta)) * cos(u * math.pi * TB)
def YFunc(R, r, u, AK, Delta, TB, Falloff, MaxRadius):
    r = HandleFalloff( r, u, MaxRadius, Falloff )
    return - (R - r * math.cos(u * math.pi / AK + Delta)) * sin(u * math.pi * TB)
def ZFunc(R, r, u, AK, Delta, TB, Falloff, MaxRadius):
    r = HandleFalloff( r, u, MaxRadius, Falloff )
    return - r * math.sin( u * math.pi / AK + Delta)
User-specified Parameters
Module = 0.6
ArcAngle = 60
TeethBeta = 6
RefRadius = 4.44
FalloffRate = 0
VerticesPerLoop = 256
Calculated parameters
total number of teeth
Teeth = (360 / ArcAngle) * TeethBeta
pressure angle is fixed
Alpha = 20 * math.pi / 180
dimensions of the worm tooth
Top = Module * ( math.pi / 2 - 2 * math.tan( Alpha ) )
Bottom = Top + 2 * Module * 2.25 * math.tan( Alpha )
A torus is defined by two radii: r And R
r = Module * Teeth / 2
R = Module *RefRadius + r
Delta
Delta1 = math.atan( Top / 2 / (r - Module) )
Delta2 = math.atan( Bottom / 2 / (r + 1.25 * Module) )
Angle coeficient
AK = 360 / ArcAngle
Code
N = int(VerticesPerLoop * TeethBeta)
verts = [[0, 0, 0] for _ in range(4 * N) ]
faces = [[0, 0, 0, 0] for _ in range(3 * (N - 1) + (N - VerticesPerLoop - 1) ) ] # the last addition (N - VerticesPerLoop - 2) is for the last set of faces we add to bridge the remaining gap.
edges = [[0, 0] for _ in range(4 * (N-1)) ]
for i in range( N ):
    # u should be in the range -1 to 1
    u = 2 * i / (N - 1) - 1
x = XFunc( R, r + 1.25 * Module, u, AK, - Delta2, TeethBeta, 0, 0 )
y = YFunc( R, r + 1.25 * Module, u, AK, - Delta2, TeethBeta, 0, 0 )
z = ZFunc( R, r + 1.25 * Module, u, AK, - Delta2, TeethBeta, 0, 0 )
verts[0 * N + i] = [x, y, z]

x = XFunc( R, r - Module, u, AK, - Delta1, TeethBeta, FalloffRate, r + 1.25 * Module )
y = YFunc( R, r - Module, u, AK, - Delta1, TeethBeta, FalloffRate, r + 1.25 * Module )
z = ZFunc( R, r - Module, u, AK, - Delta1, TeethBeta, FalloffRate, r + 1.25 * Module )
verts[1 * N + i] = [x, y, z]

x = XFunc( R, r - Module, u, AK, + Delta1, TeethBeta, FalloffRate, r + 1.25 * Module )
y = YFunc( R, r - Module, u, AK, + Delta1, TeethBeta, FalloffRate, r + 1.25 * Module )
z = ZFunc( R, r - Module, u, AK, + Delta1, TeethBeta, FalloffRate, r + 1.25 * Module )
verts[2 * N + i] = [x, y, z]        

x = XFunc( R, r + 1.25 * Module, u, AK, + Delta2, TeethBeta, 0, 0)
y = YFunc( R, r + 1.25 * Module, u, AK, + Delta2, TeethBeta, 0, 0)
z = ZFunc( R, r + 1.25 * Module, u, AK, + Delta2, TeethBeta, 0, 0)
verts[3 * N + i] = [x, y, z]


build faces array
count = 0
for j in range(3):
    for i in range(N - 1):
        index = j * N + i
        faces[count][0] = index
        faces[count][1] = index + 1
        faces[count][2] = index + N + 1
        faces[count][3] = index + N
        count = count + 1
one last thing: connect two inner loops in a tricky way, not throught the entire lengths of the loops but by removing the upper and lower loops of both sides
for i in range(N - VerticesPerLoop - 1):
    faces[count][0] = 3 * N + i
    faces[count][1] = 3 * N + 1 + i 
    faces[count][2] = 0 * N + 1 + VerticesPerLoop  + i
    faces[count][3] = 0 * N  + VerticesPerLoop  + i
    count = count + 1
createMeshFromData( 'Worm', [0, 0, 0], verts, [], faces )
create an empty at the center of the future wheel if falloff is 0
if( FalloffRate == 0 ):
    empty = bpy.data.objects.new( "wheel_empty", None )
    bpy.context.collection.objects.link( empty )
    empty.location = [R, 0, 0]
    empty.empty_display_type = 'ARROWS'
    empty.scale = [5 * Module, 5 * Module, 5 * Module]
    empty.rotation_euler = [pi / 2, 0, 0]

Here is the result in Blender: