I'm trying to figure out how a spring that looks like this behaves. I'm assuming the bottom foot can freely rotate but is otherwise fixed in position. The top foot can also freely rotate, but it is constrainted to a vertical line. The thickness is uniform. The shape of the bend isn't very important so feel free to make some reasonable assumptions about it.
Basically, I want to figure out how the distance between the feet (d) changes as a result of the force being applied.
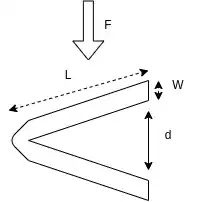
As Drew said by symetry, we calculate only the top part as an inclined cantilever beam.
To calculate the deflection of a cantilever beam inclined at an angle $ \theta $ and subjected to a load $ P $ at the free end, we use the beam deflection formula:
The deflection $ \delta(x) $ is obtained by integrating the beam's moment-curvature equation, given by: $$ \frac{d^2\delta}{dx^2} = -\frac{M(x)}{EI} $$ Where:
$$ \frac{d^2\delta}{dx^2} = \frac{P x \cos(\theta)}{EI} $$
Integrating once with respect to ( x ), we get the slope: $$ \frac{d\delta}{dx} = \frac{P \cos(\theta)}{EI} \frac{x^2}{2} + C_1 $$
Integrating again with respect to $ x $, we get the deflection: $$ \delta(x) = \frac{P \cos(\theta)}{EI} \frac{x^3}{6} + C_1 x + C_2 $$
For a cantilever beam:
Using $ \delta(0) = 0 $, we find: $$ C_2 = 0 $$
Using $ \frac{d\delta}{dx} = 0 $ at $ = 0 $, we find: $$ C_1 = 0 $$
$$ \delta(x) = \frac{P \cos(\theta)}{6 EI} x^3 $$
At the free end ($ x = L $), the maximum deflection is: $$ \delta_{max} = \frac{P \cos(\theta)}{6 EI} L^3 $$
The system is equivalent to two cantilevered beams in series, hence the deflection will be somewhere between
2 * (F * L^3/(3 * E * I)) and 2 * (F * B^3)/(3 * E * I)
where
B^2+(d/2)^2=L^2
E is the young's modulus of the spring material
I= 1/12 * W^3 * t where t is the width of the spring
