Finding change in dimensions of a rectangular bar when the bar is restricted from elongation along one cross section under uniaxial loading

Question

The question goes like this: A rectangular bar of cross-section 30mm x 60mm and length 200mm is restrained from expansion along its 30mm x 200mm sides by surrounding material. Find the change in dimension and volume when a compressive force of 180 kN acts in axial direction. Take E = $2 \times 10^7 N/mm^2$ and $\mu = 0.3$. What are the changes if the surrounding material can restrain only 50% of expansion on 30mm x 200mm side?

I understand the concept of volumetric strain and basics of elasticity. I dont understand how to approach this problem or any similar problems. I have tried many things but it is hard to visualise the problem, the more i think the more i am confused on what restriction even means.Does the diagram mean that only the front cross-section is restricted and the cross-section in the back is free to elongate? I believe that when the cross section given along x and z direction is restricted from elongating, expansion should take place along y-axis but that would mean that the dimensions of z and x would vary which is not possible as it is restricted. Please help me through this,it is enough if i could gain knowledge to tackle such problems on my own.

Answer 1

I am sure this question was posed as a retaliation to some students acting up. I changed the young modulus to that of steel $ 2*10^5$.

Part 1: Fully Restrained Expansion

• Given Data:

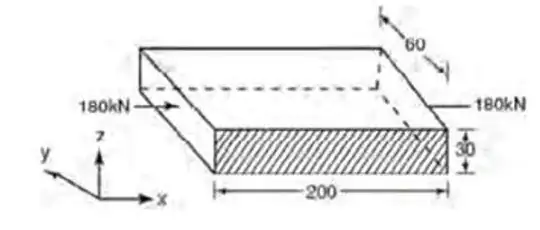
Cross-section: $30 mm * 60 mm$

• Length (L): $200 mm$
• Compressive Force (P): $ 180kN = 180,000N $
• Young's Modulus (E): $2 \times 10^5 \text{ N/mm}^2$
• Poisson's Ratio ($\mu$): $0.3$

Calculate axial stress ($\sigma$):

$$ Area (A) = 30 * 60 = 1800 mm $$

$$ \sigma = \frac{P}{A} = \frac{180,000N}{1800 mm^2} = 100 N/mm^2 $$

Calculate the axial strain ($\epsilon_x$):

$$ \epsilon_{x} = \frac{\sigma}{E} =\frac{-100 N/mm^2}{2*10^5 N/mm^2} = -0.0005 $$

Calculate Change in Length ($\Delta L$): $$\Delta L = \varepsilon_x \times L = -0.0005 \times 200 mm = -0.1 mm$$ Calculate Lateral Strain ($\varepsilon_y$, $\varepsilon_z$):

Since the 30 mm side is fully restrained,

$\epsilon_y = 0$. $$\epsilon_z = -\mu \times \epsilon_x = -0.3 \times (-0.0005) = 0.00015$ (tensile) $$ Calculate Change in Width ($\Delta z$): $$\Delta z = \epsilon_z \times 60 mm = 0.00015 \times 60 mm = 0.009 mm (increase) $$ Calculate Change in Thickness ($\Delta y$):}

Since the 30mm side is restrained, $\Delta y = 0 mm$.

Calculate Change in Volume ($\Delta V$):} \begin{itemize} \item Original Volume (V) = $30 mm \times 60 mm \times 200 mm = 360,000mm^3$

Final Volume (V') = $(30 mm \times (60.009 mm) \times (199.9 mm) = 359,946 tmm^3$

$\Delta V = V' - V = 359,946mm^3 - 360,000 mm^3 = -54mm^3$ (decrease) $

Part 2: $50\%$ Restrained Expansion

Steps 2-4 are the same as in Part 1:

• $\sigma = 100mm^2$
• $\epsilon_x = -0.0005$
• $\Delta L = -0.1mm$

Calculate Lateral Strain ($\epsilon_y$):}

If fully unrestrained, $\epsilon_y = -\mu \times \epsilon_x = 0.00015$

With 50% restraint, $\epsilon_y = 0.5 \times (-\mu \times \epsilon_x) = 0.5 \times 0.00015 = 0.000075$

Calculate Change in Thickness ($\Delta y$):}

$\Delta y = \epsilon_y \times 30 mm = 0.000075 \times 30 mm = 0.00225 mm$ (increase)

Calculate Lateral Strain ($\epsilon_z$):}

$\epsilon_z = -\mu \times \epsilon_x = 0.00015$ (same as Part 1)

Calculate Change in Width ($\Delta z$):}

$\Delta z = \epsilon_z \times 60mm = 0.00015 \times 60 mm = 0.009 mm$ (same as Part 1)

Calculate Change in Volume ($\Delta V$):

Original Volume (V) = $360,000mm^3$

Final Volume (V') = $(30.00225 mm) \times (60.009mm) \times (199.9 mm) = 359,973 mm^3$

$\Delta V = V' - V = 359,973 mm^3 - 360,000 mm^3 = -27 mm^3$

Summary of Changes:

Fully Restrained:

• $\Delta L = -0.1 mm$
• $\Delta y = 0 mm$
• $\Delta z = 0.009 mm$
• $\Delta V = -54 mm^3$

$50\% $Restrained:

• $\Delta L = -0.1 mm$
• $\Delta y = 0.00225 mm$
• $\Delta z = 0.009 mm$
• $\Delta V = -27 mm^3$

I may have arethmatic errors; I did not check it!