I am working on a system that consists of a hanging-pendulum thrust balance with two pivot points, one in the front and one in the back There is a heavy weight applied in the front. I can change the position of the center of gravity by applying counterweights on the rear part. See attached image.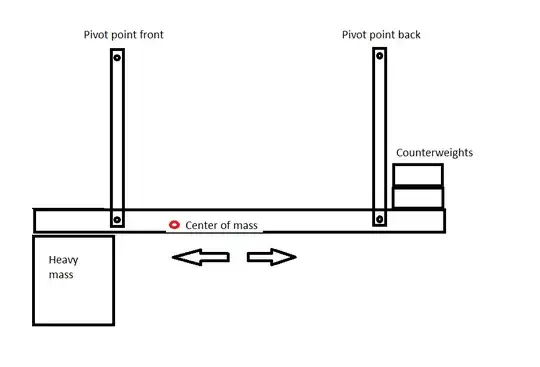
. The position of the center of gravity is known as well as the moments of inertia with respect the pivot points
I would like to simplify this system to an equivalent physical pendulum with one pivot point. However, because I have two pivot points, I have two moments of inertia, one with respect to each one of the pivots.
In the beginning I thought about taking the mean average of both, and then calculate the period of a physical pendulum or compound pendulum, just as Hyperphysics suggests: $T=2\pi\sqrt{\frac{I_{y}}{mgLcm}}$, where
- $I_{y}$ is the average moment of inertia,
- $m$ is the mass of the system,
- $L_{cm}$ is the distance pivot-center of mass.
but this just does not seem right. Can somebody give me a hint on how to do this? Better, is it even reasonable to do such simplification? Shall I use a matrix notation? My purpose is to study how the thrust balance will respond when a force is applied upon it.
I have analyzed the oscillations of the system for several counterweights. From the study of those oscillations I can obtain the damping coefficient $\zeta$ and the natural frequency of the undamped system $\omega_{n}$, but I still need $I_{y}$ to complete the equation $\omega_{n}=\sqrt{\frac{k}{I_{y}}}$.
