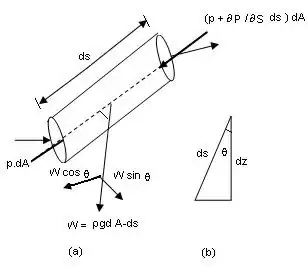
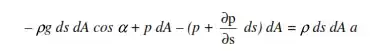For the last hour I have been trying to understand what $\dfrac{\partial p}{\partial s}ds$ is in Euler's equation but I have a problem. You can see this image:
I know that $p\ dA = \text{Force}$
$γ ds dA = mg$
but what is $\left(p + \dfrac{\partial p}{\partial s} dA\right)$?