Automotive Radiator Simulation

Question

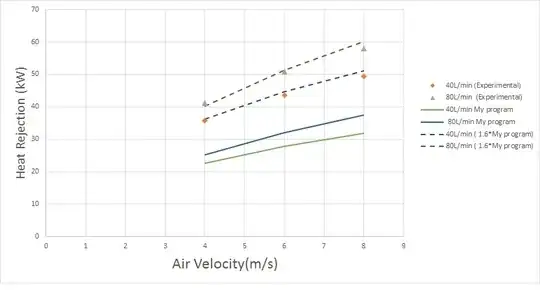
I'm developing a code to simulate thermal performance of automotive radiators.

My results are 40% under-predicted. But when I multiply them to 1.6, they match completely.

This is the graph that compares the results of program and experimental work.

It should be noted, this number (1.6) differs when we use the other data sets.

Procedure of the program is as following :

given air velocity, coolant flow rate, inlet air and coolant temperatures.
assume outlet air and water temperatures (it should be a logical assumption).
calculate air and fluid properties (using interpolation in existing tables based on mean temperatures)
calculate heat transfer coefficient of water according to flow regime (using Petukhov or Gnielinski equations)
calculate Colburn j factor (using Chang and Wang empirical correlation)
calculate the total thermal resistance between air and coolant.
calculate NTU and effectiveness
Calculate heat rejection
Calculate outlet temps and compare them with assumed temps. If it doesn't meet the specified error, go to step 3 and repeat calculations.

clc;clear all
% _____Jung Experiment_______
% Air Velocity m/s
    Va=4;
water_Flowrate=2e-3/3;% m3/s (40 L/min)
% Top tank and inlet air temperatures (deg C)
twih=85; t_ambient=25;
% Specifying the j-factor correlation (Chang & Wang)
cor='CW';
% Entering the Radiator characteristics
cas='C:\Users\Solid\Desktop\jung.xlsx';

% ___ Calculation ___
ITD=twih- t_ambient;
% Export Geometrical details from jung.xlsx file and calculate the needed
% Areas like AT(total heat transfer area etc).
[R,L,Afrt,Afrf,Ac,Afront,sigma,Af,Aw,AT...
    Lp,Fp, Fl, Ll, alpha, Fd, Tp, deltaf, Nlb,Td,LH,af,Dh,NT,kf...
    RH,RW,RD,N,Nct,Np,Nf,Yl,Dm,D_major,W,tt]=Area_Calc(cas);
% Radiator tubes are flat. So we need hydraulic diameter(dw). 
[dw,A_cross,Perimeter]=hydro2(Dm,L);
% ___ Pre_Procssing ___ 
t_top_tank=twih;
twi= t_top_tank;
tai = t_ambient;
%  defining an error;
error=.01;
% Assuming outlet temperatures of water(Two) and Air(Tao) logically.
Tao=50; Two=75; 
Y=1; 
% defining a counter;
ll=0;
        while Y
            Q=0;
        ll=ll+1;
%         At the end of the loop, calculated temperatures will be         compared
%         with the tepms of the past iteration.So we save the tepms of     the
% past iteration here.  
        Two1=Two; Tao1=Tao;
% Calculating the properties like viscosity(uw(coolant),ua(air)),Prandtel
% Number (Pra(air) ,Prw(coolant)) etc.
        [ uw,ua,rhow,rhoa,cw,ca,kw,ka,Prw,Pra,tam ]=...
            phyprop2(twi ,tai,Two,Tao);
%       Air side Reynolds number. ReLp is the reynolds number based on
% Louver pitch. 
        ReLp=rhoa*Va*Lp*1e-3/(ua);
        ReDh=rhoa*Va*Dh*1e-3/(ua);
%         Air mass flowrate
mair=Ac*rhoa*Va;

% --- Coolant side Reynolds number and mass flowrate ---
[Rew,mwater]=hydro(dw,A_cross,water_Flowrate,rhow,uw,...
    NT,'I');
% coolant heat transfer coff.
[hw]=hc2(Yl,dw,Rew,kw,Prw,1);
% Air heat transfer coff. and friction factor
% (friction factor(f) will be calculated but won't used in this program )
[ha,jcor,f]=ha2...
    (Lp,Fp,Fl, Ll, alpha,Fd, Tp, deltaf, Nlb,Td,LH,Dh,ua,rhoa,ca,Pra,...
    Va,cor,ReLp,ReDh,Dm,tt);
 % ----------- UA , NTU--------
 l=Fl*1e-3/2;
M=sqrt(2*ha/(kf*deltaf*1e-3));
% fin and Surface efficiency
nf=tanh(M*l)/(M*l);
no=1-Af*(1-nf)/(AT); Q=0;
% ----------Capacity Rate-----------
Ca=mair*ca; Cw=mwater*cw;

if min(Ca,Cw)==Ca
Cmin=Ca;
Cmax=Cw;
Q=1;
else
Cmin=Cw;
Cmax=Ca;
end
Cs=Cmin/Cmax;
% Calculation of overall heat transfer coefficient using thermal
% resistances between air and water(fouling and wall resistances are
% negligible)
UA=(( 1/(hw*Aw)+1/(no*ha*AT) ) )^-1;
NTU=UA/Cmin;
% -------------  E - NTU (calculation of effectiveness _epe_ using         existed 
% correlations) -----------------
epe=eps1(Q,N,Cs,NTU,Cmin,Ca);
% Air and water outlet temps
tao=tai+epe*Cmin*(twi-tai)/Ca;
two=twi-epe*Cmin*(twi-tai)/Cw;

Tao=tao;
Two=two;
% do these temps meet the errors ?
Y=abs(Tao-Tao1)/Tao>error2 ||...
    abs(Two-Two1)/Two>error2;
        end
%         Radiator Heat Rejection
        q=epe*Cmin*ITD;
        disp(q)

What's wrong?

score 2 · Answer 1 · answered Jan 21 '16 at 10:29

Either your definition of "completely" is a bit unusual, or there's something wrong with those charts, because in those charts, 1.6 x the model does not completely match any of the six observations you have (assuming the point values are at the centre of each shape).

Either way: your model outputs don't match your observations, with or without a 1.6 fudge factor.

So it's some combination of:

your assumptions don't match reality;
your inputs don't match reality;
your model doesn't match reality;
your observations don't match reality;
there are things outside the system boundary of your model that are crucial to the results, that you are not accounting for (this is kind of a subset of the first bullet point).

So, you need to go through, step-by-step, verifying or correcting each of those.

At a first guess: have you actually calibrated your model at any point: that is, taken a set of inputs that you can be absolutely sure of, and a set of observations that you can be absolutely sure of, and got a match. Or is what you're presenting to us, actually an uncalibrated model - in which case, why should it look like reality? The second-best way to tackle this: does your model reproduce the results of some other, calibrated model?

Automotive Radiator Simulation

1 Answers1