Please take a look at following figure:
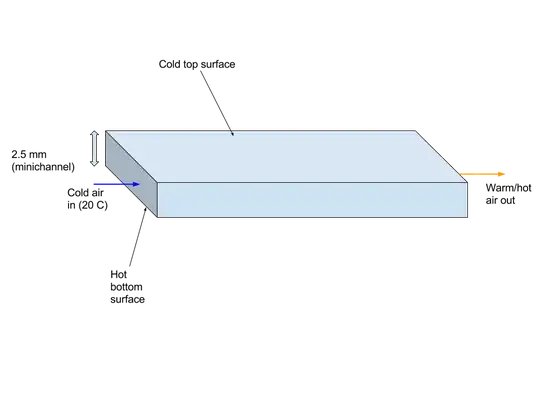
System considered is a narrow rectangular channel of 2.5 mm depth (W x L is 60 mm x 150 mm). Since channel has low depth, it can be considered as mini-channel. Bottom surface is hot and at $~ 100\,^o \text{C}$, top surface is initially at ambient $20\,^o \text{C}$. Air flow enters channel at $20\,^o \text{C}$. I want to know how for such narrow channel heat transfer is defined for air as working fluid. Specifically: $$ Nu = f(Re, Pr)$$ a correlation of Nusselt number as function of Reynolds and Prandtl number. Re range is in 500 - 2000. Any suggestion of literature reference are welcome.