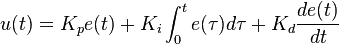PID controller explanation

Question

I haven't found a text that explains the PID controller in simple words. I know the theory: that it calculates the derivative and the proportional gain and the integral etc, but I need to know in reality what is the output of each function and each combination of functions.

For example, starting with the proportional: it sends an input that is proportional to the error recorded. So if the error is 5 V, does it do $\frac{1}{2}\cdot5\text{ V}$ to diminish it? or $\frac{1}{5}\cdot5\text{ V}$? or $-\frac{1}{5}\cdot5\text{ V}$ or what? I don't understand.

As for the derivative, it monitors the derivative across a specific time? And then does what? Also, what if there is a noise/disturbance at the begining, so the PID controller will not have normal use rates of change to compare? Same with integral. Can you point me to a good resource or explain me please?

Answer 1

A PID function that most people use every day is the hand-eye coordination to steer a car or bicycle. Your eyes are the input, the angle of the steering wheel/handle bars is the output. The set point is usually the center of your lane (until a deer hops out or a dog chases you).


Your mind has to constantly consider 3 different factors when preforming this task. The importance it places on each factor is based on past experience, which is called "tuning" in the PID world.

Proportional: "I am a long ways from the center of the lane, I should turn back that direction."
Naturally, if I am further away I want turn sharper than if I am very close. This will allow me to get back to the center of my lane in a timely manner.

Derivative: "I better not just yank the wheel/ handle bars over that direction or I will over-correct, roll, and crash."
You may be in the gutter, but your driving experience teaches you that if you turn sharply things will change very quickly and you need to reduce how sharp you turn to keep from over shooting your set-point and entering on-coming traffic.

Integral: "The wind keeps pushing me to the edge of the road, and I have to turn into it to stay on coarse"
You are pretty close to the center of your lane, but not quite where you want to be. Proportional is small because you are really close and Derivative is small because you are not changing very fast. Integral is the term that steps in and says "Hey now, I know we are not off by much but we have been off for a pretty long time; how about we turn into the wind so we can hold our set point."

PID's aren't perfect, and your steering abilities are actually quite a bit better than a standard PID. You are smart enough to realize that when the wind disappears (for some unknown reason) you zero out your integral term and don't wander into opposing traffic while waiting for the wind to come back. Humans also self tune during operation by considering other inputs like accelerations and physics, while most machines/computers are not currently capable of this.

Answer 2

In intuitive terms I have found the following explanation to be useful.

For the sake of argument lets say that our system is filling a bucket with a hole in it water from a tap. We measure the depth of water in the bucket and control the flow rate of water via a tap. We want to fill the bucket as quickly as possible but don't want it to overflow.

The proportional element is a linear measure, in this case the height of the water in the bucket this is a useful measure of how full the buck is at a given time but it tells us nothing about how quickly it is filling so by the time we notice it is full it may be too late to turn off the tap or if we fill it too slowly water will leak through the hole faster than it fills and it never quite gets full.

On paper this sound s like it should be enough on it's own and in some cases it is, however it break down when the system itself is inherently unstable (like an inverted pendulum or a fighter jet) and the lag between measuring the error and the input taking effect is slow compared to the rate at which external noise induced perturbations.

The derivative element is the rate of change of the water level. This is especially useful when we want to to fill the bucket as quickly as possible eg we might open the tap as far as it will go at the start to fill it quickly but close it off a bit once the level gets near the top so we can be a bit more precise and not over fill it.

The integral element is the total volume of water added the bucket. If the bucket has straight sides this doesn't matter much as it fills at a rate proportional to the flow of water BUT if the bucket has tapered or curved sides then the volume of water in it starts to have an effect to the rate at which the water level changes. More generally because this is an integral it accumulates over time so applies a greater response if the P and D elements aren't correcting enough eg by maintaining the bucket at half full.

Another way to look at this is that the integral is a measure of the cumulative error over time and is effectively a check on how effective the control strategy is at achieving the intended result and is able to modify the input depending on how the system really behaves over a period of time.

So in summary :

the P (proportional) element is proportional to the variable that you want to control (like a simple thermostat)

the D (derivative) element is proportional to the rate of change of that variable

the (integral) element is perhaps the most difficult to understand but relates to the quantity that your P parameter is measuring typically this will be a cumulative quantity like volume, mass, charge, energy etc.

Answer 3

PID controllers use tuning parameters to adjust the response.

From the equation for PID control:

The three K-subscript terms are the tuning parameters, and there's one for each term of the PID controller output: proportional, integral, and differential.

So, for example, with an error of +5V and a Kp of 0.3, the output would be 1.5V. Likewise for the integral and differential terms.

In practice, these parameters are determined experimentally. The Ziegler-Nichols (pdf) tuning method is a simple heuristic method that used to be very popular in industry.

These days, most off-the-shelf PID controllers and PLC functions have built-in tuning.

Hope that helps!