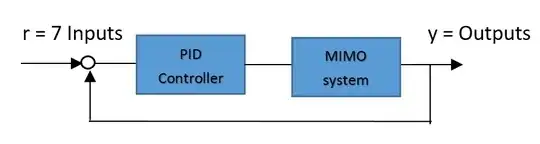
How do you design a PID controller for MIMO systems in which the outputs outnumber the inputs?
It's typical to design a PID controller for MIMO industrial process with the same number of inputs and outputs, or with more inputs than outputs. And very few references talk about systems with less inputs than outputs. However, there are lots of chemical process where this is normal.
Is there any analytical method except (square down ans nrga) to design a PID controller for system with more outputs than inputs? I've considered a lot of references but haven't found anything!
Where Mimo sys matrixes are: (Matlab defiend programm)
A = [-6.932e-2,17.41,-36.75,0,0,0,-6.0660,-31.54,0;
-1.435e-4,2.719e-2,-1.411e-3,3.467e-1,0,-9.380e-1,7.139e-2,-1.691e-2,0;
-4.537e-4,1.870e-3,-2.025e-1,0,1,0,-4.688e-2,7.563e-3,0;
-1.304e-4,-7.179,-4.916e-1,-6.172e-1,-3.689e-2,7.631e-1,0,0,0;
2.297e-5,0,-8.667e-1,4.393e-2,-1.947e-1,-2.026e-2,0,0,0;
1.964e-5,4.263e-2,-1.329e-2,1.233e-3,1.579e-2,-1.600e-1,0,0,0;
0,0,0,1,1.941e-1,2.771e-1,0,6.258e-2,0;
0,0,0,0,8.192e-1,-5.736e-1,-5.612e-2,0,0;
0,0,0,0,6.055e-1,8.648e-1,0,2.006e-2,0]
B = [0,0,-7.560,9.067e-4;
-6.952e-3,1.293e-2,0,0;
0,0,-3.425e-2,-9.577e-7;
4.249,5.989e-1,0,0;
0,0,-1.796,0;
-7.287e-2,-2.877e-1,0,0;
0,0,0,0;
0,0,0,0;
0,0,0,0]
C = [0,-5.758e-1,0,0,0,0,0,0,0;
0,0,0,1,0,0,0,0,0;
0,0,0,0,0,1,0,0,0;
0,0,1,0,0,0,0,0,0;
0,1,0,0,0,0,0,0,0;
0,0,0,0,1,0,0,0,0;
0,2.719e-2,-1.411e-3,3.467e-1,0,-9.380e-1,7.139e-2,0,0]
D = [-1.298e-1,-1.610e-1,0,0;
0,0,0,0;
0,0,0,0;
0,0,0,0;
0,0,0,0;
0,0,0,0;
-6.952e-3,1.293e-2,0,0]
Gss = ss(A,B,C,D)
G = tf(Gss)
The forth input of Mimo sys is Constant.