Where did I go wrong conceptually when attempting to calculate the maximum force on a truss at a given joint?

Question

In the problem statement below, the question states to find the maximum load $\vec{P}$ that the truss can support. My method of approach was:

1. Draw a FBD for the entire structure.
2. Generally I would identify all external forces, however for this problem I felt it was unnecessary because I felt they weren't needed if I knew already the forces in each member.
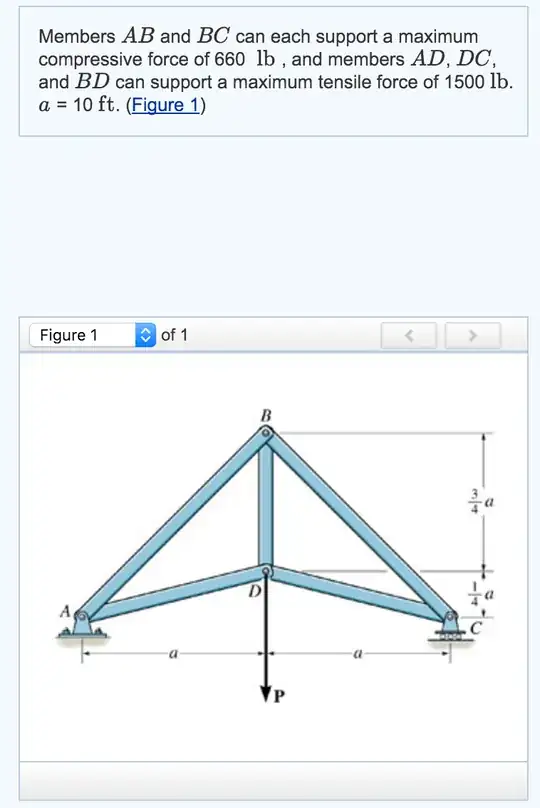
3. So I then dove straight into joint $D$, and assumed each member connected to $D$ was in tension and experienced the maximum tensile force $\vec{T} = 1500$ lb.

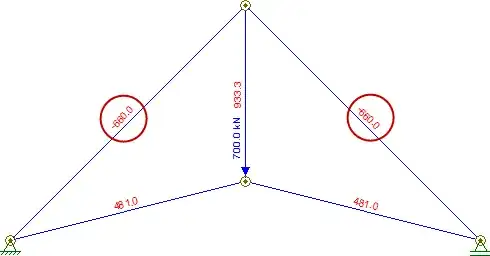
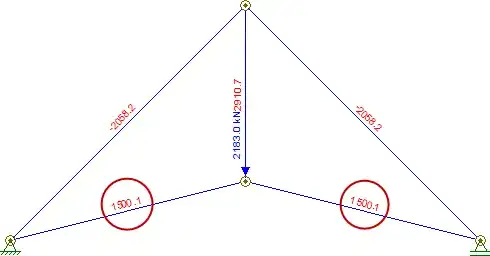
However, this led to the wrong answer when solving for $\vec{P}$. The solution manual instead found each external force in terms of $\vec{P}$ and started at joint $A$ to find $\overrightarrow{AD}$ and $\overrightarrow{AB}$ in terms of $\vec{P}$. In addition, in order to get numerical values, the solution manual assumed member $\overrightarrow{AB}$ was experiencing the maximum compression force of 660 lb. However, when I assume that member $\overrightarrow{AD}$ is experiencing the maximum tensile force, it doesn't work out the same.

My question is, conceptually, why must I find each each member's force in terms of $\vec{P}$, and why must one assume $\overrightarrow{AB}$ is experiencing maximum compression (but not $\overrightarrow{AD}$ in maximum tension)?

EDIT: I want to note that I do not need help with solving this problem, nor the math required. I simply am just looking for a conceptual answer as to why my approach did not work (i.e. only analyzing joint $D$).

Answer 1

The reason is that you assumed that the elements around node $\text{D}$ will be the first to fail. That is not the case. Indeed, it is the elements under compression ($\text{AB}$ and $\text{BC}$) that will fail first. Also, you assumed that all the members around $\text{D}$ will present the same axial force, which is untrue.

To see this, here's your structure with a unitary load (the units are irrelevant):

And here are the axial forces in each member under this unitary force (positive in tension):

Since these results are linearly proportional to the force applied, we can now find the concentrated load $P$ at node $\text{D}$ that each member can withstand:

$$\begin{align} P_{\text{AB}} = P_{\text{BC}} &= \dfrac{660}{0.943} = 700 \\ P_{\text{AD}} = P_{\text{CD}} &= \dfrac{1500}{0.687} = 2183 \\ P_{\text{BD}} &= \dfrac{1500}{1.333} = 1125 \\ \end{align}$$

Therefore, the maximum load supported by the structure is the minimum of these values, which is 700 lb.

To show the validity of these results, let's now apply each of these forces and check the results in the relevant members:

_{All results obtained with Ftool, a free 2D frame analysis program.}