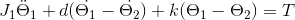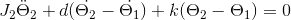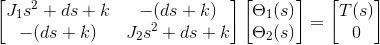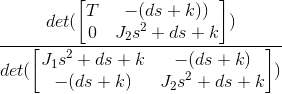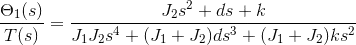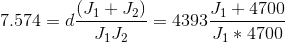6

I have a double mass rotary model. The two masses are connected by an axis which together acts as a spring damper system of the fourth order. The system is actuated by a motor and the angle of rotation is measured by rotary encoders at each end of the mass. The input to the motor is milli-volts which then converts into corresponding torques. The output measured is angle of rotation of the mass. The actuation and the measurement is on the same side. The system looks similiar to this

enter image description here

The transfer function from output to input of the system is,

$Plant = \large {\frac{(4700 s^2 + 4393 s + 3.245 (10)^8)}{(s^4 + 7.574 s^3 + 1.202(10)^5 s^2)}}$

Is it possible to determine the mass of the system from the transfer function or bodeplot? How can I relate the voltage, torque, mass and angle of rotation?

idkfa
  • 1,734
  • 1
  • 11
  • 19
Somanna Thapanda
  • 95
  • 6

1 Answers1

1

I'm going to derive the transfer function symbolically from the differential equations you provided in the hopes that you might be able to extract the rotational moment of inertia (not the mass directly, you'd have to know the radius of the rotating masses) from the formula.

Here are the equations of motion as I interpreted them from your comment. J1 is the mass that the torque is applied to.

Equation of motion for mass 1

Equation of motion for mass 2

Taking the Laplace transform and writing in matrix form:

enter image description here

I will use Cramers' method to determine the transfer function for mass 1, the mass to which the torque is applied:

enter image description here

This transfer function Theta1/tT can be expressed as:

enter image description here

Comparing this to your experimentally determined transfer function indicates that the rotational moment of inertia for mass 2 is 4700, and d is 4393. Using algebra you can solve for J1:

enter image description here

Solving for J1 should give about 672.3891.

If you want to check my math, here is a simple Matlab code I used:

j1 = sym('J1');%moment of inertia mass 1
j2 = sym('J2');%moment of inertia mass 2
d = sym('d');%damping coefficient
k = sym('k');%spring constant
t = sym('T');%applied torque
s = sym('s');%laplace variable

%system matrix
A = [j1*s^2+d*s+k -(d*s+k);-(d*s+k) j2*s^2+d*s+k]

det(A)

Acramer = [t -(d*s+k);0 j2*s^2+d*s+k]

det(Acramer)
willpower2727
  • 725
  • 4
  • 12