1

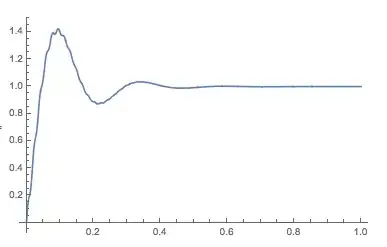
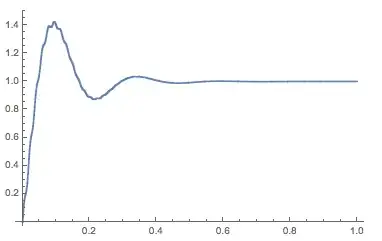
I have trasfer functions of a plant and a controller in laplace domain. I checked for the closed loop response by applying a step response. The system is found to be stable.

I checked the response of the system for the same step reference in discrete domain. I can see that the closed loop response of the discrete system is unstable. The transfer function is converted to discrete form by c2d option in matlab with a sampling time of 1ms.

Shouldnt the response of the system be same in both continuous and discrete domain (atleast for high sampling frequency)?

Somanna Thapanda
  • 95
  • 6

1 Answers1

2

The plant and controller: $$\text{sys}=\frac{4700 s^2+4393 s+3.245\times 10^8}{s^4+7.574 s^3+120200. s^2}$$

$$pid=0.287\, +0.008 s+\frac{0.5}{s}$$

The closed-loop system obtained as $\frac{pid*sys}{1+pid*sys}$:

$$csys=\frac{37.6 s^4+1384.04 s^3+2.59961\times 10^6 s^2+9.31337\times 10^7 s+1.6225\times 10^8}{1. s^5+45.174 s^4+121584. s^3+2.59961\times 10^6 s^2+9.31337\times 10^7 s+1.6225\times 10^8}$$

The poles are all in the left-hand plane:

$$ \{-11.8643\pm \, 346.642 i,-9.80897\pm \, 25.3345 i,-1.82737\}$$

Thus as expected, the response to a unit-step is stable:

enter image description here

The zero-order hold approximation for a sampling period of 1 ms: $$ \frac{-0.0371234 z^4+0.144584 z^3-0.213662 z^2+0.141976 z-0.0357747}{-1. z^5+4.83687 z^4-9.46905 z^3+9.38322 z^2-4.70688 z+0.955831}$$

The poles are all within the unit-circle:

$$ \{0.929426\pm \, 0.335734 i,0.989921\pm \, 0.0250846 i,0.998174\}$$

Again, as expected, the response to a unit-step is stable (and the plot is essentially the same):

enter image description here

Suba Thomas
  • 2,036
  • 11
  • 15