4

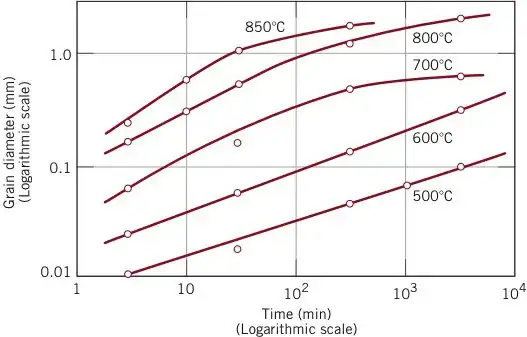
An uncold-worked brass specimen of average grain size 0.009 mm is heated to 600 degrees Celsius for 1000s, what is the average grain size based on this graph?

enter image description here

How to tackle this problem? I don't know if I am using the graph correctly. My approach was:

1000s is 16.67 min, $\log(16.67) = 1.22$

So $\frac{22}{100}$ between 10 and 102. Which is about 0.67 cm to the right of 10 on x-axis.

Now lets estimate this corresponds to 10-1.333 on the y-axis of the 600 degrees celcius graph line. So 0.046 mm.

But this does not seem correct, because I did not incorporate the 0.009 mm starting position. Which corresponds to heat treatment time of about 1 min at 600 degrees so should I add 1 min to the 1000s? And thus look look at the point on the graph at 17,76 min?

The answer in book seems way off, they talk about average grain size 0.2 mm. To me that seems like they looked at the graph of 700 degrees Celsius.

grfrazee
  • 3,597
  • 1
  • 18
  • 33
strateeg32
  • 517
  • 3
  • 13
  • 21

2 Answers2

2

Grain growth is the movement of grain boundaries by diffusion to reduce the grain boundary area. This graph tells that at 600 degrees, a treatment of one minute shall give the y coordinate of the 600 degrees graph. So treating a sample for 1000s shall mean heating the sample at 600 from time t=0.0. The starting point is inherent in the process itself.

RTh
  • 131
  • 4
1

The recrystallization temperature for brass is <400 Celsius (Harding et al., 1980), so the original microstructure won't affect the results here.

Your process seems good, and my guess would be the answer in the book was either from the 700 Celsius line or 1000 min on the 600 Celsius line.

Adam Nekimken
  • 86
  • 2