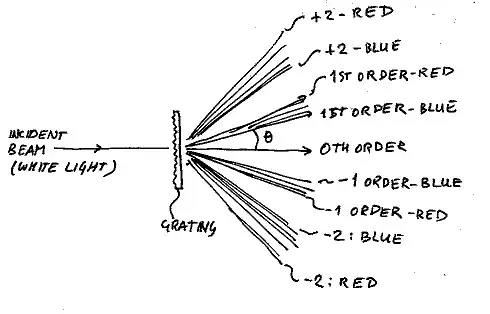
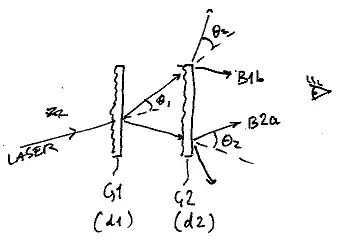
Double diffraction is where a light beam passes through an grating with distance D1 between ridges and then passes through an grating with distance D2 The image after passing through diffraction gratings is a function of the product of two Fourier tranforms in the frequency domain. In other words, the product of two Fourier transforms in the frequency domain is equivalent to the convolution of the two Fourier integrals in the time domain.
If we match spatial coherence length for a given wavelength with the spacing between the diffraction grating ridges, what is the intensity of the image after passing through two cascaded diffraction gratings each with distinct spacing between grating ridges?
The reason I ask this question is to examine the best linear combination of 2 cascaded diffraction grating where the 2 unique diffraction gratings are centered around 2 of the primary colors, red green and blue. For example, suppose we want to filter an orange laser pointer in the far field(i.e 100 meters) to protect pilot's vision from the orange laser pointer or dual wavelength laser pointer upon takeoff or landing.
Each of the diffraction gratings would be centered at a fixed visible light wavelength. Would it be necesssary for one of the cascaded diffraction grating to be centered around a variable visible light wavelength harnessing the Pockels effect where a varying electric field modulates the electro-optic behavior of the diffraction grating aperture radius?
Please excuse my novice use of terminology and suggest how I should modify my presentation if you have time.
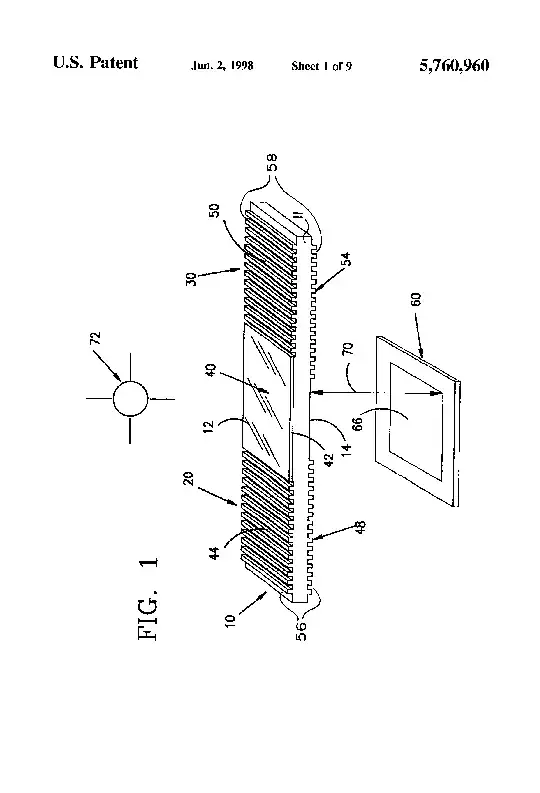
Dr. Chih-Hsien Jason Lin, Ph.D and Dr. Yu-wha Lo , Ph.D of the Cornell Research Foundation filed U.S. Patent 5760960 A, "Cascaded self-induced holography", in June 1998 which harnesses Young's Interference experiment with diffraction gratings. This excellent research may be used to deflect and filter laser pointer beams in the visible light region. Cambridge University Press published a book , Optical coherence and quantum optics, by Professor Leonard Mandel and Professor Emil Wolf of the University of Rochester,around the same time analyzing the complex spatial coherence function from Young's two slit interference experiment using Fourier integrals. Pages 171 to Page 176 of this seminal book directly address the analysis of spatial coherence and optical filters for Young's two slit interference experiment
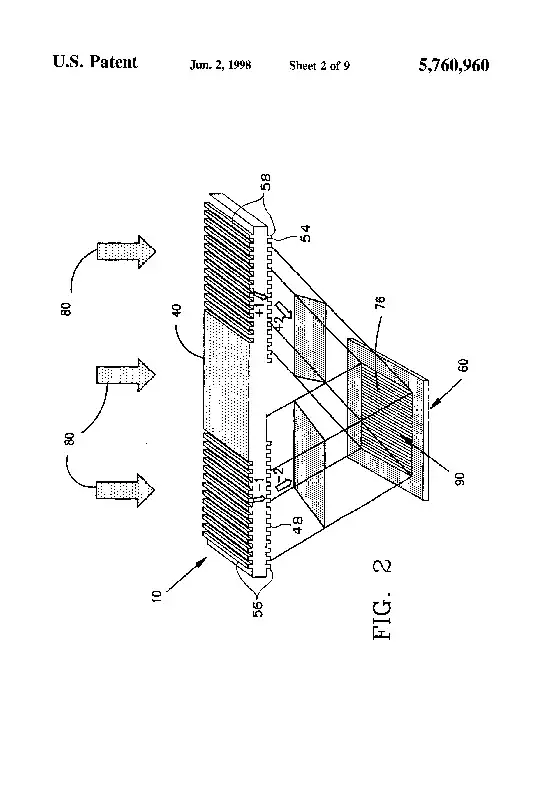
"FIG. 2 illustrates that the size of the central opaque region 40 defines a target exposure area 76 on the substrate 60 by shading the target area 40 from direct illumination by the light source 72. This allows only the interference patterns from the cascaded grating pairs 56 and 58 to reach the target area 76. Preferably, the size of the target area 76 can be from a few millimeters to a centimeter square, and is comparable to the exposure size for an optical stepper."
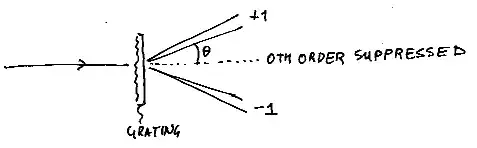
"The linearly polarized monochromatic light from the light source 72 indicated at 80 is first diffracted by the first and third mask gratings 44, 50 on the top surface of the mask 10. Most of the photon energy is contained in the first order diffraction beams labeled as +1 on the right and -1 on the left. Other diffractive beams and the zero order transmitted beams are not shown in FIG. 2 because they do not play a role in the final grating formation. When the +1 and -1 diffraction beams reach the second and fourth mask gratings 48 and 54 on the bottom of the mask 10, two new diffracted beams labeled as +2 and -2 are generated. As shown in FIG. 2, the target area 76 is the area where only the desired +2 and -2 beams can interfere, thereby exposing a grating 90 which has a period of approximately 1/4 of the periods in the mask gratings 44, 48, 50 and 54."
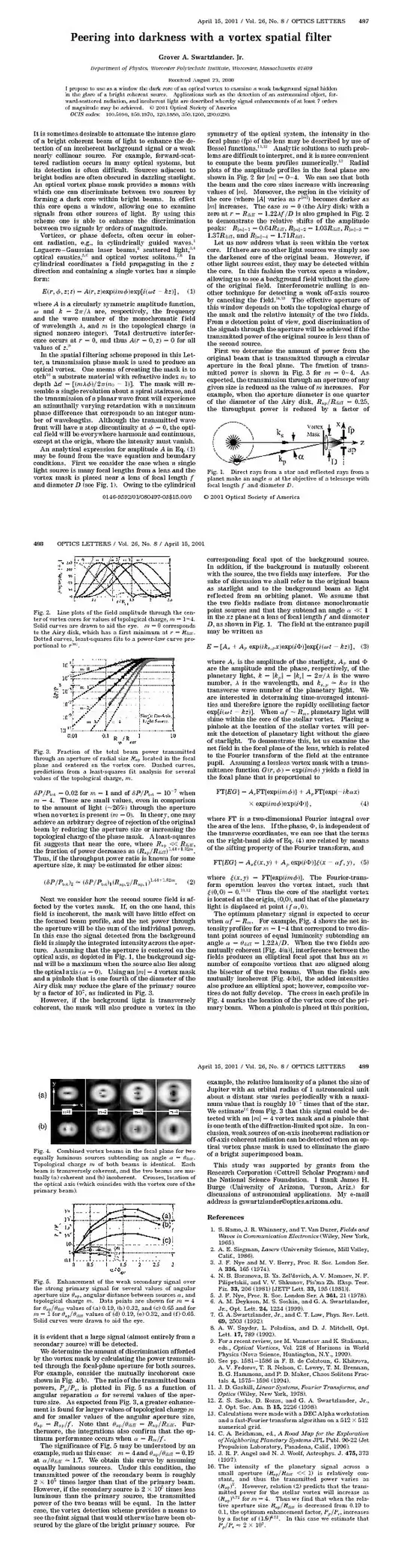
Grover A. Swartzlander wrote in 2000 in the attached article , "Peering into Darkness with a vortex spatial filter" , at the bottom of this question that "It is sometimes desireable to attenuate the intense glare of a bright coherent beam of light to enhance the detection of an incoherent background signal or a weak nearly collinear source". I would like to extend this research to protecting airline pilots from the effects of laser pointers shone from the ground at planes on takeoff and landing. The reason I wish to enhance the detection of a weaker incoherent background signal is to image this signal on a Planar transparent display.