Algorithm to determine fastest route?

Question

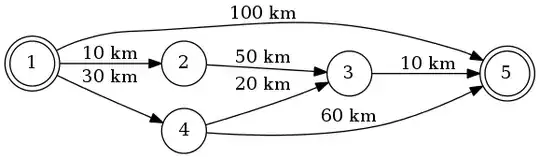
Let's say we're going from 1 to 5. The shortest route will be 1-4-3-5 (total: 60 km).

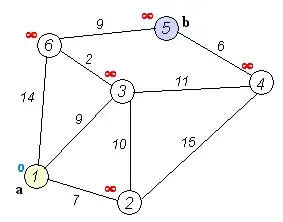
We can use Dijkstra's algorithm to do that.

Now the problem is, the shortest route is not always the fastest one, because of traffic jams or other factors.

For example:

• 1-2 is known to have frequent traffic jams, so it should be avoided.
• Suddenly a car accident happens along 4-3, so it should be avoided too.
• Etc...

So probably we can speed on the route 1-4-5, because of no traffic jams/accidents, so will arrive at 5 faster.

Well that's the general idea, and I haven't think about more details yet.

Is there any algorithm to solve this problem?

Answer 1

Yes: Dijkstra

Dijkstra works just as well for this situation.
You just use time rather than distance as the weight of each arc.

Answer 2

Yes. Dijkstra's algorithm will solve this problem.

The problem in your case is that you automatically assume the shortest path equates to distance travelled, when in fact it more appropriately equates to the COST of taking a route.

If one path has a roadblock then its COST should be higher, and the algorithm still applies.

Answer 3

You should just be able to replace your distance with the time between nodes and solve it the same way.

Answer 4

Dijkstra

As said before, it is not only used for shortest distance. I believe this animation gives a good understanding of the "power" (for lack of a better word) of Dijkstra:

Answer 5

Since you brought congestion into the picture, be careful you don't get caught by Braess' Paradox. If everyone chooses the optimal path, it results in worse travel time for everyone.