8

I'm working with a weighted, undirected multigraph (loops not permitted; most node connections have multiplicity 1; a few node connections have multiplicity 2). I need to find the shortest path between two subgraphs of this graph that do not overlap with each other. There are no other restrictions on which nodes should be used as start/end points.

Edges can be selectively removed from the graph at certain times (as explained in my previous question) so it's possible that for two given subgraphs, there might not be any way to connect them.

I'm pretty sure I've heard of an algorithm for this before, but I can't remember what it's called, and my Google searches for strings like "shortest path between subgraphs" haven't helped. Can someone suggest a more efficient way to do this than comparing shortest paths between all nodes in one subgraph with all nodes in the other subgraph? Or at least tell me the name of the algorithm so I can look it up myself?

For example, if I have the graph below, the nodes circled in red might be one subgraph and the nodes circled in blue might be another. The edges would all have positive integer weights, although they're not shown in the image. I'd want to find whatever path has the shortest total cost as long as it starts at a red node and ends at a blue node. I believe this means the specific node positions and edge weights cannot be ignored.

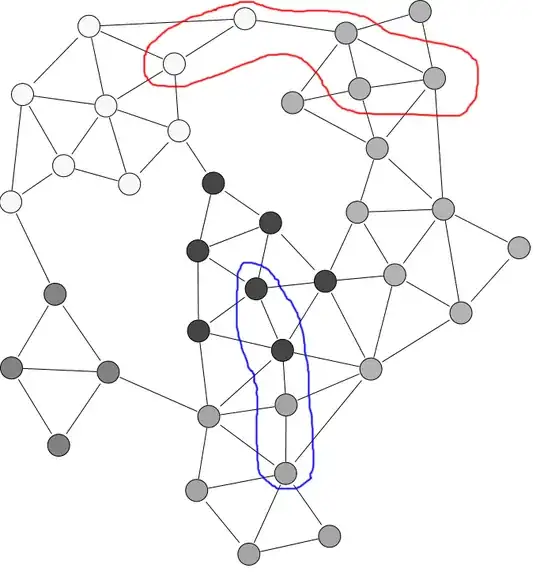
enter image description here

(This is just an example graph I grabbed off Wikimedia and drew on, not my actual problem.)

Community
  • 1
Pops
  • 4,123
  • 4
  • 29
  • 41

2 Answers2

5

You should be able to adapt Dijkstra's algorithm.

Just add two points A & B to your graph, which are connected to one of the subgraphs each. Then calculate the shortest path between the two points A & B.

The shortest path between the two subgraphs should be the path that you get after removing A & B from the result.

Jens Schauder
  • 1,513
1

After struggling for a day trying to shoehorn fake nodes and edges into my poorly designed code, I'm beginning to think that SJuan76's suggestion is really quite elegant. I can't prove that it works in all cases, but I've run through a few examples by hand and it seems to do okay.

Start with plain old Dijkstra's Algorithm. Make the following minor changes:

  • The regular algorithm sets all initial distances to infinity other than "the source node." Instead, set all initial distances to infinity. Then, change the distance to zero for each node in the "start" subgraph. (For an undirected graph like mine, you can just pick either subgraph.)

  • Keep running the algorithm normally until the only nodes that remain in the unvisited set are nodes in the "end" subgraph. It's safe to stop at this point because they can only possibly make distances larger, not smaller. (If you have negative edge weights, this doesn't apply.)

  • Look through all of the nodes in the "end" subgraph, and pick the one that has the lowest total score. That's the end node.

  • Follow the path of saved "previous node" info until a node in the "start" subgraph is reached.

Pops
  • 4,123
  • 4
  • 29
  • 41