3

For this 2d grid (black square are not penetrable, white square are):

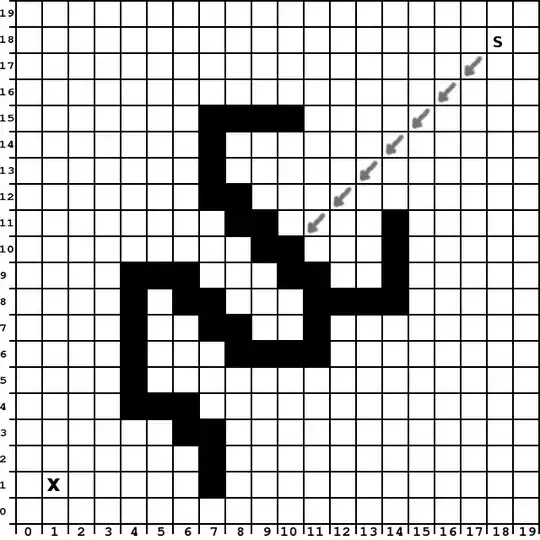
enter image description here

I want to find path who permit to move an object to a start point (x:18, y:18) to a end point (x:1, y:1), square by square. Imagine this object is an ant or a robot, so:

It can only know the direction of its objective, distance from its objective and if around (1 square distance) square are penetrable or not. Object can keep memory of its path, if it is bypassing because previously blocked, etc ...

  • At (x:18, y:18), ant know X direction is (x:-1, y:-1) vector, distance from X is 18 square, vector (x:-1, y:-1) is penetrable).
  • At (x:17, y:17), ant know X direction is (x:-1, y:-1) vector, distance from X is 17 square, vector (x:-1, y:-1) is penetrable).
  • ...
  • At (x:11, y:11), ant know X direction is (x:-1, y:-1) vector, distance from X is 11 square, vector (x:-1, y:-1) is not penetrable).
  • ?

But it can't know other things. So we can't use here an A* algorithm or Dijkstra's algorithm. Imagine object is a robot in your house. It can test every position like Dijkstra's algorithm but it will take two week to bypass a chair.

Which algorithm can be used to find path from S to X without "walking" on a black square, according to "ant"/"robot" limitations ?

I write some, but with some problems like difficulty to follow "wall" and
go round in circles ...

UPDATE: After Karl Bielefeldt response, i write alogithm available here and procuding: EDIT: I finally not use A* inspiration, but "follow wall inspiration"

AntStar pernal slgorithm

You are free to fork and suggest enhancement !

bux
  • 133

2 Answers2

5

If you are allowed to remember past data, A* is indeed your best bet. I used it on Google's Ant AI challenge, which only has a small radius of view.

The main difference with a limited field of view is you do a lot more walking around just to explore, but that's unavoidable. A* will give you a pretty good list of where to explore, without having to visit the entire map.

For fun, I coded a solution for your example. The following is the output:

(18,18)
(17,17)
(16,16)
(15,15)
(14,14)
(13,13)
(12,12)
(11,11)
(11,10)
(10,11)
(9,12)
(8,13)
(8,14)
(8,13)
(9,12)
(10,11)
(11,10)
(12,9)
(13,9)
(13,10)
(13,11)
(14,12)
(15,11)
(15,10)
(15,9)
(15,8)
(14,7)
(13,6)
(12,5)
(11,4)
(10,3)
(9,2)
(8,1)
(7,0)
(6,1)
(5,1)
(4,1)
(3,1)
(2,1)
(1,1)

real    0m0.404s
user    0m0.727s
sys     0m0.040s

It's even more efficient than I anticipated. Only 40 moves, when the ideal with an omnipotent view of the map would be 25. You can see it follows your arrows at first, explores along the wall to the Northwest a little, then turns around and follows the wall until it escapes the indentation, after which it's almost a straight shot. It could maybe be improved even further by tweaking the weights on unseen cells to be proportional to distance from your current position.

Karl Bielefeldt
  • 148,830
1

It looks like you are looking for an A* or Dijkstra algorithm.

Depending on the language you are working with, there is likely already libraries built that you can use for these. Here is a some Pseudocode for A* algorithm and an example for Dijkstra's algorithm

EDIT: Although Dijkstra would technically work, it wouldn't nearly as efficient as it should be.

Zachary Dow
  • 165