4

Since this question is not about "code not working", I'm asking my first question here instead of StackOverflow. Inform me if any required information is missing from the question.

Setup:

I have two dictionaries of type Dictionary<int, int> where the keys are a range from 1 to n and the values are the frequencies of those numbers. For example:

var frequenciesA = new Dictionary<int, int>
{
    { 1, 3 },
    { 2, 5 },
    { 3, 4 }
};

var frequenciesB = new Dictionary<int, int>
{
    { 1, 1 },
    { 2, 3 },
    { 3, 4 }
};

Input:

Now I will get a list of integers as an input, in the range of 1 to n, like this:

var numbers = new List<int> { 1, 2, 3, 3, 2, 1, 1, 2, 3, 1, 2, 2 };

I also create a frequency-dictionary from this list with following code:

var frequenciesFromInput = Enumerable.Range(1, 3)
                                     .ToDictionary(x => x,
                                                   x => numbers.Count(y => y == x));

This would result in following key-value pairs:

K  V
----
1  4
2  5
3  3

Problem:

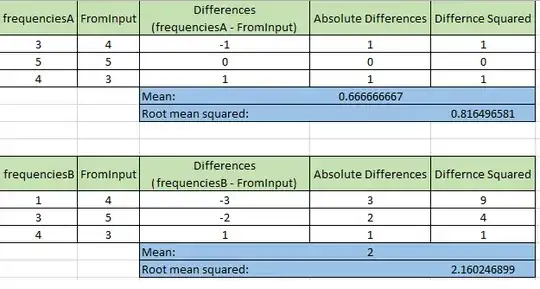
Suppose I needed to determine to which from the other dictionaries (A or B) the frequencies equals, that'd be easy: take the values of the dictionaries as a list and use the Enumerable.SequenceEqual<T> method.

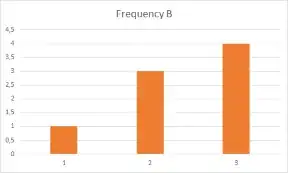
But in my case I need to determine which dictionary (A or B) matches closest to the frequencies of the input dictionary. Visualizing this makes it easier to understand. Here are the charts for the constant frequencies of dictionary A and B:

Chart for frequency AChart for frequency B

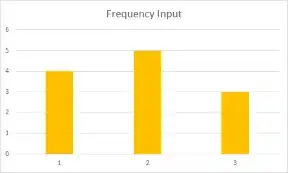
And here's the chart of the input dictionary:

Chart for frequency of input

As you can see the frequencies of A match closer than to those of B.

Question:

How would I start creating a method/algorithm to determine which dictionary (A or B) is closer to that of the input dictionary. I'm not asking for a full implementation, just a little push as for now I have no idea where and how to start on this.

Only thing I could think of was some variation on the Knapsack problem, but I'm not sure I'm on the right path there.

Abbas
  • 543

3 Answers3

3

Vector subtraction should be enough. And find the mean (or root mean square) of the absolute differences-- the smaller, the closer match.

EDIT:

Example: enter image description here

** Root mean squared = Sqr(Sum(xi²)/n) where xi are Differences

kunthet
  • 313
2

The googleable name for your problem is creating a statistical classifier. It's quite a large topic. You can try a basic vector subtraction like kunthet's answer and see if it works for your application. However, if you end up with a lot of incorrect classifications, there are many considerations that can drastically improve the accuracy of your classifier.

For example, perhaps you have a bunch of documents, and you want to know if they were written by Pharrell or Shakespeare. Straight vector subtraction will disproportionately weight words with large coincidental frequency differences like the word the, compared to less frequent words that are much more useful in classification, like forsooth or happy. There are feature extraction algorithms that can determine those more useful words automatically, and classification algorithms that can weight them appropriately.

By all means, try the simple algorithm first. Just be aware there are a lot of subtle pitfalls in this sort of problem, that you might have to delve deeper to solve.

Karl Bielefeldt
  • 148,830
1

Since the data can be considered vectors, vector arithmetic offers a simple solution. This approach has the advantages of either allowing the use of an existing vector library or creating a vector library, which you can then use for other projects.

"Closest" is a question of distance. There are various metrics that give distance between Cartesian vectors, but the most common is the Euclidean, ℓ₂. Euclidean distance can be defined in terms of more basic vector operations.

Start with vector subtraction, which is done component-wise: the difference of vectors is the vector of differences. In a sense, subtraction distributes across vectorization. Symbolically:

<xᵢ> - <yᵢ> = <xᵢ - yᵢ>

You also have a componentwise product:

⃑x * ⃑y = <xᵢ*yᵢ>

Next is the dot product (·), which is the sum of the components of the componentwise product:

⃑x · ⃑y = ∑(⃑x * ⃑y)ᵢ

The Euclidean norm (norms in math are abstract length functions) is the square root of the dot product:

‖⃑x‖ = √(⃑x · ⃑x)

Note the Euclidean norm is basically the Pythagorean theorem in n-dimensions, which you can see by expanding operations:

‖⃑x‖ = √(∑(⃑x * ⃑x)ᵢ) = √(∑(xᵢ²)) = √(x₀²+x₁²+...+x₏²)

Finally, the Euclidean distance is the Euclidean norm of the difference:

ℓ₂(⃑x,⃑y) = ‖⃑x - ⃑y‖

Finding the closest vector from a collection is the generic min function: loop over the collection, keeping track of the item (here, vector) with the smallest value (here, distance) seen thus far.

See also the least squares method, which is nearly equivalent but is in terms of functions rather than vectors and omits taking the square-root (which isn't necessary for this particular problem).

outis
  • 1,171