eg, with the dollar, you never have precision of less than $0.01
Oh really?

the age old issue of why you shouldn't store currency as an IEEE 754 floating point number.
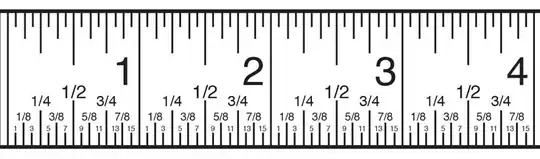
Please feel free to store inches in IEEE 754 floating point numbers. They store precisely how you'd expect.
Please feel free to store any amount of money in IEEE 754 floating point numbers that you can store using the ticks that divide a ruler into fractions of an inch.
Why? Because when you use IEEE 754 that's how you're storing it.
The thing about inches is they're divided in halves. The thing about most kinds of currency is they're divided in tenths (some kinds aren't but let's stay focused).
This difference wouldn't be all that confusing except that, for most programming languages, input into and output from IEEE 754 floating point numbers is expressed in decimals! Which is very strange because they aren't stored in decimals.
Because of this you never get to see how the bits do weird things when you ask the computer to store 0.1. You only see the weirdness when you do math against it and it has strange errors.
From Josh Bloch's effective java:
System.out.println(1.03 - .42);
Produces 0.6100000000000001
What's most telling about this isn't the 1 sitting way over there on the right. It's the weird numbers that had to be used to get it. Rather than use the most popular example, 0.1, we have to use an example that shows the problem and avoids the rounding that would hide it.
For example, why does this work?
System.out.println(.01 - .02);
Produces -0.01
Because we got lucky.
I hate problems that are hard to diagnose because I sometimes get "lucky".
IEEE 754 simply can't store 0.1 precisely. But if you ask it to store 0.1 and then ask it to print then it will show 0.1 and you'll think everything is fine. It's not fine, but you can't see that because it's rounding to get back to 0.1.
Some people confuse the heck out of others by calling these discrepancies rounding errors. No, these aren't rounding errors. The rounding is doing what it's supposed to and turning what isn't a decimal into a decimal so it can print on the screen.
But this hides the mismatch between how the number is displayed and how it is stored. The error didn't happen when the rounding happened. It happened when you decided to put a number into a system that can't store it precisely and assumed it was being stored precisely when it wasn't.
No one expects π to store precisely in a calculator and they manage to work with it just fine. So the problem isn't even about precision. It's about expected precision. Computers display one tenth as 0.1 the same as our calculators do, so we expect them to store one tenth perfectly the way our calculators do. They don't. Which is surprising, since computers are more expensive.
Let me show you the mismatch:

Notice that 1/2 and 0.5 line up perfectly. But 0.1 just doesn't line up. Sure you can get closer if you keep dividing by 2 but you'll never hit it exactly. And we need more and more bits every time we divide by 2. So representing 0.1 with any system that divides by 2 needs an infinite number of bits. My hard drive just isn't that big.
So IEEE 754 stops trying when it runs out of bits. Which is nice because I need room on my hard drive for ... family photos. No really. Family photos. :P
Anyway, what you type and what you see are the decimals (on the right) but what you store is bicimals (on the left). Sometimes those are perfectly the same. Sometimes they're not. Sometimes it LOOKS like they're the same when they simply aren't. That's the rounding.
Particularly, what do we need to know to be able to store values in some currency and print it out?
Please, if you're handling my decimal based money, don't use floats or doubles.
If you're sure things like tenths of pennies won't be involved then just store pennies. If you're not then figure out what the smallest unit of this currency is going to be and use that. If you can't, use something like BigDecimal.
My net worth will probably always fit in a 64 bit integer just fine but things like BigInteger work well for projects bigger than that. They're just slower than native types.
Figuring out how to store it is only half the problem. Remember you also have to be able to display it. A good design will separate these two things. The real problem with using floats here is those two things are mushed together.




