0

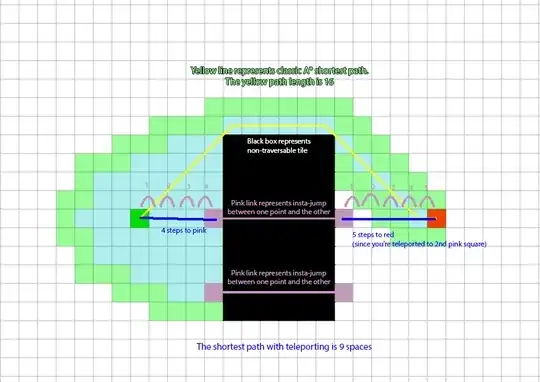
How would I implement a shortcut finder into an A* path-finding algorithm? Assume that every tile is represented by an (x,y) coordinate, and I know where every "good" tile and every "non-walkable" tile is on the grid. How could I best find the solution to this problem on a large scale where the starting and ending spots are always different with many different shortcuts and obstacles in the way of each starting point and ending point. What is the most optimal way of finding the shortest path between grid points miles away (assuming each tile represents 1 foot)?

Description

Community
  • 1
Jeff smith
  • 341

2 Answers2

2

A* cannot generally be used with shortcut/jump nodes. This is because A* uses a heuristic, roughly: “walking into the direction of the target is the optimal route, barring any obstacles”. Or more formally: the triangle inequality must hold. The triangle inequality guarantees that taking a detour will result in a longer path. The A* algorithm relies on a heuristic that never underestimates the minimum distance.

However, jump nodes violate this assumption. It is possible to construct a scenario where the shortest path is to run away from your target in order to find a jump node. So the A* heuristic can be misleading. In your example the jump nodes would happen to work fine because they are in line with the direction suggested by the heuristic, but this is not generally the case.

If you want to use A* with jump nodes, you need to adapt the path-finding algorithm to not only search a path towards the target, but also to all jump nodes that are closer than the target (as informed by your heuristic). This is complicated (because you have to update the list of possible jump nodes after a jump) but efficient. Alternatively, you can use a different path finding algorithm, e.g. Dijkstra (which is A* without a heuristic, so a breadth-first search).

Representing the jump nodes is not difficult if you write your A* algorithm in terms of nodes rather than in terms of grid coordinates. Given a node, you will have a neighbours(node) operation that gives its neighbours. These neighbours are typically neighbouring grid points. However, the function can take into account jump nodes, and return the jump target's neighbours instead.

amon
  • 135,795
0

A* is applicable wider than squared grids.

Rather than defining the neighbours of a tile to be only those that differ by one in the X or Y direction, you include any shortcuts and exclude any obstacles.

Start from the pseudocode on Wikipedia

function neighbours(node)
    result := []
    for displacement in [(1,0), (-1,0), (0,1), (0,-1)]
        neighbour := node + displacement
        if passable(neighbour)
            result.Add(neighbour)
    for shortcut in shortcuts[node]
        result.Add(shortcut)
    return result

Then you need to make sure that your distance heuristic never overestimates.

function prepare_heuristic(shortcuts, goal)
    result := Infinity
    for node in shortcuts.values
        result := min(result, displacement(node, goal))
    return result

function distance_heuristic(node, goal)
    return min(shortcut_distance, displacement(node, goal))

This is still an improvement over pure Dijkstra, especially when shortcuts are rare

Caleth
  • 12,190