What algorithm should I use for this game problem?

Question

I have a grid-based puzzle game, that is based on states. I need an algorithm that can find a solution for each game level. A game level starts in a specific state and ends in a unique, well-known state, so I need to find a path to walk from the start state to the end state.

Each object in the game grid can be moved in 4 directions and only stops when it collides with another object; and each move represents a unique, well-defined state. The game level is solved when all objects are positioned in their pre-specified locations, which is the puzzle part of the game. The game rules are extremely simple, but finding the solution for a level seems very hard.

Specifications of the problem

• Each state cannot be randomly predicted or generated. It must derive from (be a child of) another previous state.
• There is no effective way to measure how close we are to the goal state. We only know we reached the end when we find it.
• There can be too many possible states. In average, there are about 32^100 possible states per each game level.
• Many of the states, have derived states that are also their ancestral states. For example, we can get stuck on a cycle that never ends.
• We cannot traverse the states from the goal to the start state — i.e. we can't walk back.
• Many of the states can lead to a dead end, where it isn't possible to reach the end state.
• The number of states per level is limited — i.e. the number of object moves per game level is limited, so the found solution must be within this limit.

What I have tried

• I tried a brute force tree-based custom algorithm, but the possible states are too many. This algorithm works well for the simpler game levels, and it can find the shortest path between the two states. However, for complex game levels (which are most of the levels), this algorithm doesn't work, because it's brute force.
• I tried genetic algorithms. Although there is no effective way of measuring how close are we to the goal state, there is some score that can be obtained when certain objects are moved in certain ways. Higher score means we are closer to the end state, but can also get us in a dead end, which is what happens most times, as game levels are designed on purpose for that. I used this score as a measure for fitness. The genetic algorithm works more or less good for simple game levels, but it isn't reliable in most of the complex ones. Also, due to the nature of the problem, there is no way I can think of to implement crossover; and mutation is very hard to implement as well.
• I looked at (but not tried) some path-finding algorithms, like A*, but they rely on a "how close are we to the goal?" property, which this problem doesn't really have.

So, in the face of a problem like this, is there an algorithm that is a good candidate for finding solutions for these game levels? I guess Deep Learning approaches would work well for this, but that would be too much for this game, as hardware resources are somewhat limited.

EDIT 1 — An example 3rd party game

The game I'm making is, in concept, similar to this game. This game is based on a game called Q, which I only know from an old Sony Ericsson cell phone — one of the first cell phone models that had a color screen. The game I'm sharing as example, that is in Microsoft Store, is the only replica I could find; I couldn't find any online version, sorry about that. The game I'm working on has the same rules, but has additional objects that add different rules, to make the game more interesting (like objects that make balls stop, objects that make balls change direction, etc.).

If you play it, you may notice a human solves it using mostly reason, because each level has different geometries for the walls, some balls need to be put in their slots in some order, for the level to be possible to be solved, etc. With additional objects that add more complexity, solving the levels requires the human to understand some key ingredient specific to that level. For example, sometimes a ball is stuck in some place, and the key may be using one of the other balls together to take it out of there. There are some basic strategies that are helpful for most levels, but they alone cannot solve the levels. The most simple levels are pretty straightforward to solve, but there are ones (usually the most interesting) that require the human to be smart and use reason and some creativity to put all the balls in their respective slots.

Unfortunately, the game I'm working on is a work in progress, and is not yet functional on the visual part, so I can't yet use it as an example.

EDIT 2 — Some example game levels

I managed to produce some pictures of some example levels for the game. They are the following, in order of hardness (well, more or less):

---

This level is fairly simple. Balls can be potted inside the squares with matching color, just like the 3rd party example game above.

---

This level is not very hard, but the mine in the center makes it tricky. Mines are objects you should not move over them, or else you lose the game.

---

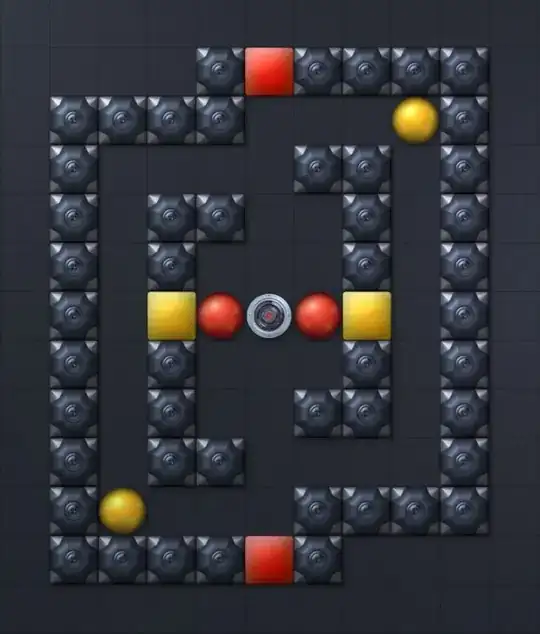
This level is tricky, because balls are stuck within the geometry of the level, and avoiding potting balls is key. To solve this level, a lot of collaboration between all balls is necessary.

---

This level is limited to a maximum of 60 moves. That is what makes it a bit harder. The magnets make balls stop when moved through, but they are consumed (i.e. one time use). The square in the center is an Iris slot — any ball can be potted inside it. The key for solving this level within the maximum number of moves is to choose ball routes wisely.

---

This is the hardest level in these examples. The boots (a pickable item), once consumed, add 10 extra moves to the moves limit. The three boot items, add 30 extra moves in total. To solve the level you need to consume them, or else you run out of moves. But going for the boots will also spend some moves as well, so it requires a careful strategy. The little brains and the X2 are just optional pickable items that give some score.

---

Answer 1

My first thought for solving this was indeed A*. I cannot tell whether this is feasible or not, since this really depends on the number of states, the number of steps to get there and how well the heuristic works for this specific problem. An example level would help.

I looked at (but not tried) some path-finding algorithms, like A*, but they rely on a "how close are we to the goal?" property, which this problem doesn't really have.

I want to challenge you here. What you need is a good heuristic to give you a lower bound for the number of moves needed to go to a solution. Assuming that your game is similar this game there is different ways to have heuristics that provide lower bounds. Some of them might involve simpler problem solving algorithms themselves.
One such heuristic might be:
For each piece calculate the minimum number of moves to move it to the goal state, assuming that all other pieces are placed in the most convenient way. The sum of the moves needed for each piece is a lower bound for the total moves needed.

Whether this will be enough to get to a solution in your specific case is hard to tell without concrete example.

Answer 2

I've written several solvers for games like this, and I usually start with a simple state space search. Assuming that you have the concept of a GameState, it should support generating all valid child GameStates possible from that state, and telling if a GameState is unsolvable (i.e. because a Ball has fallen in the wrong hole) or if it is the solution. Also, every GameState should have a reference back to its parent state so if you've found the solution, you can trace back its moves.

Solving the game then boils down to performing a breadth-first search using a Queue, and will return the optimal solution if there is one:

public GameState Solve(GameState initialState)  {
Queue<GameState> queue = new Queue<GameState>();
queue.Enqueue(initialState);

while (queue.Count > 0) {
    GameState gs = queue.Dequeue();
    Move[] moves = gs.GenerateAllValidMoves();

    foreach (Move move in moves) {
        GameState childState = new GameState(gs, move);

        if (childState.IsSolution())
            return childState;

        if(childState.IsUnsolvable() == false)
            queue.Enqueue(childState);
    }
}

return null;  //No solution exists.

}

Preventing duplicate work

Obviously this is a rather naive approach, and for all but the most simple GameStates this will produce far too many child GameStates. As you mentioned yourself, child GameStates can form cycles, and some pairs of moves produce the same GameState (i.e. Move A left, Move B down can produce the same GameState as Move B down, Move A left).
In other words, we're doing a lot of duplicate work, and this is magified by the fact that it's not just one GameState that we've already seen before, but also the entire tree of child GameStates that we'll be pointlessly processing too.

The best way to prevent this is to keep track of all GameStates we've encountered so far, and to only process GameStates that we've not seen before:

public GameState Solve(GameState initialState)  {
    Dictionary<GameState, GameState> knownGameStates = new Dictionary<GameState, GameState>();
Queue&lt;GameState&gt; queue = new Queue&lt;GameState&gt;();
queue.Enqueue(initialState);

while (queue.Count &gt; 0) {
    GameState gs = queue.Dequeue();
    Move[] moves = gs.GenerateAllValidMoves();

    foreach (Move move in moves) {
        GameState childState = new GameState(gs, move);

        if (childState.IsSolution())
            return childState;

        if(childState.IsUnsolvable() == false) {
            if (knownGameStates.ContainsKey(childState) == false) {
                knownGameStates.Add(childState, childState);
                queue.Enqueue(childState);
            }
        }
    }
}

return null;  //No solution exists.

Packed GameStates

Once you start tracking several million(?) GameStates, memory will likely become an issue. Most likely your GameState class is very suitable for producing valid child moves, but contains several member fields and references to other objects that make it not very compact in terms of memory usage. At this point it pays to define a PackedGameState that, apart from the parent reference and its hash code, only contains a byte array containing the most dense representation possible of a game state.

The Dictionary and Queue should then store PackedGameStates, and only when you Dequeue() a PackedGameState it should be converted back into a GameState so we can do smart things with it. Conversely, every generated child state gets serialized into a PackedGameState before it is queued.

At this point you should have a pretty decent algorithm that is capable of solving at least some of the more simple games.

PriorityQueue

But that's not to say you can't refine it further. Instead of using a regular Queue (which was basically ordered on the Depth of the GameStates, that is, the number of moves from the initial GameState) you could use a PriorityQueue, where the priority is determined not only by the Depth but also maybe the number of Balls remaining - the idea being that these GameStates are closer to the solution and therefore more promising and should be explored first. You might have to toy with how you weigh the Depth and the number of Balls remaining into a single priority value that works well.

This makes for a more 'guided' search (a bit like A*) and will probably produce a solution faster, but since you're no longer doing a regular depth-first search, the solution produced need not be optimal in terms of number of moves, so you probably should continue searching for a better solution.

Branch and Bound

At this point, you can refine the algorithm even further using a Branch and Bound approach, provided you can devise a way to determine how many moves a particular GameState needs at minimum to be solved, just by looking at that GameState.
For example: every Ball that is aligned on either the X or Y axis of the Hole it belongs in takes at least 1 move, if its not aligned on either axis it takes at least 2 moves. Summing this for all Balls left in the GameState produces the minimum number of moves needed. It will most likely need more moves than this because of how the GameState is layed out, but never less than that.

Now, say that you've found a solution and are looking for a better solution, the way to use this is that if the current GameState's Depth + MinimumNrOfMovesRemaining is equal or greater than the current solution's Depth, then this GameState can never produce a better solution than we already have, and therefore shouldn't be queued to be explored further.
Including this condition in the algorithm means that the PriorityQueue will eventually run empty, at which point you know you've found the optimal solution.

Answer 3

I'm going to answer the "How do you choose an algorithm/approach a problem" angle on this question rather than just solving your example game.

For problems you expect a human to be able to solve you can ask yourself "how do I solve these problems" Humans don't generally solve by brute force.

If its Like Chess or Go The way humans solve these kind of problems is by reducing the search space with assumptions.

In chess for example we can say that some moves are obviously good. Taking an unprotected piece, moving an attacked piece etc, these are the moves a human looks at first, and we can replicate that in a computer by assigning value to moves or positions and trimming the search by removing moves which are "bad" before we get to the end of the game.

Or Maybe its like a Rubiks cube and there are ways to move a piece without changing the positions of the others. You can then construct a solution by adding together these blocks of steps. A human learns the steps and works back from the goal state and this can be replicated in a machine with dynamic programming, ie solving a small version of the problem is a building block to bigger versions of the problem.

Or Maybe it's like Sudoku and there is a trick, which once you know you can apply to solve any grid.

Or maybe its like poker where there is hidden knowledge you have to guess at and you can make the most probable guess for perfect play.

If your game really is the impossible "brute force is the only solution" problem you suggest then it cant be fun for humans to solve?