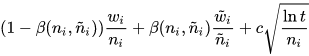8

I've written an implementation of the UCT1 Monte Carlo Tree Search algorithm for selecting moves in a two-player game. In the future, I'd like to expand this implementation to use more advanced tree search techniques like RAVE to be able to search more efficiently. I'm trying to figure out how to write unit tests for this kind of highly complex "black box" code.

The basic idea of monte carlo search is to play thousands of random games and select promising search nodes based on previous game outcomes. The basic pseudocode for tree search (from "A Survey of Monte Carlo Tree Search Methods" by Browne et al.) would be:

function UCTSEARCH(s₀)
 create root node v₀ with state s₀
 while within computational budget do
   v₁ ← TREEPOLICY(v₀)
   ∆ ← DEFAULTPOLICY(s(v₁))
   BACKUP(v₁, ∆)
 return (BESTCHILD(v₀, 0))

Using a Tree Policy to find a node in the tree which has not previously been explored, a Default Policy to score that node, e.g. by playing random games until termination, and a backpropagation step to apply reward values to parent nodes. Various algorithms exist to modify each of these steps, e.g. the selection function for RAVE (per wikipedia) maximizes

RAVE node selection

I'm finding it very difficult to write unit tests for code of this nature. From the perspective of a caller of this function, its behavior is opaque and non-deterministic, since it relies on random number generation. I also want to expand and modify the algorithm in the future, meaning all the implementation details are likely to change over time.

What strategy would you use to write unit tests for an algorithm like this?

Derek Thurn
  • 189

3 Answers3

6

it relies on random number generation

This is easy to solve - you ensure your code uses a pseudo-RNG for which you can precisely the seed the state. You now have deterministic behaviour.

(You should almost certainly be doing this anyway, or you are adding to the replication crisis)

Philip Kendall
  • 26,027
6

This seems like a proper use case for Property Based Testing, a la Haskell's QuickCheck. In property based testing, you start by thinking of properties you expect your code to have. For instance, if you were testing a function to reverse the order of a list, you might brainstorm the following

  1. The reverse of a list has the same length as the list.
  2. The reverse of the reverse of the list is identical to the original list.
  3. The reverse of a list has the same elements as the list.
  4. etc.

You would then have test cases which generate random lists and check whether these properties hold, failing and printing the offending cases. If your function is nondeterministic you would also want to print out a seed on failure so that you can replicate these failures.

Note that so long as you state these properties in ways that depend only on the externally visible behavior of your code rather than its implementation details, you can treat your code as a black box. Similarly, careful choice of properties can ensure the tests are robust against improvements to the code.

The language you are implementing this in may or may not have a library like QuickCheck. If it does not, it is simple enough to rig one up. All you need is some code for randomly generating inputs to your method and a unit testing system. Robust property based testing libraries like QuickCheck will have some features that help to generate minimal counterexamples to properties, which can make it easier to understand what is failing and why. This comes down to having a notion of size of input (starting small and gradually generating larger inputs) and functionality to shrink a counterexample to try to find a smaller one.

walpen
  • 3,241
5

How do you eat an elephant? One bite at a time.

What I am trying to say here is, for unit testing a complex algorithm like Monte Carlo Tree Search, it is probably best not to treat it in a black-box fashion as a single unit.

As you scetched in your question, this algorithm has some clearly separated parts. Each of its parts ("Treepolicy", "Defaultpolicy", "Backup", "Bestchild") has a clear input and output, hence it can (and probably should) be unit tested on its own (this works best when those parts are not implemented in a procedural fashion, but in a functional one). Note only one of those steps ("Defaultpolicy") has non-deterministic behaviour, which can be approached by replacing the non-deterministic pseudo-random generator by a deterministic one during tests.

Of course, once you finished your unit tests, you can also add integration tests afterwards to test the algorithm "as a whole". That can help you to verify the integrated units work together and produce some result of the desired form. However, since you wrote

I also want to expand and modify the algorithm in the future, meaning all the implementation details are likely to change over time.

an integration test against some expected output will only be of restricted value. Such tests can help you finding regressions when you are going to change things often in the algorithm which shall not change the results, but in this case, you are going to experiment with modifications of this algorithm where the results will be different and cannot easily predetermined. Hence, as long as you are experimenting with it, it will be probably more efficient to do the integration tests manually or "semi-automatic".

Instead, when you experimenting with different treepolicies, you want to be sure you don't change accidentally something in the other parts. This could happen, for example, when for implementing a different treepolicy you may have to change something in a common, underlying component (for example, the tree data structure). That's where unit test for the other components show their value.

Or, lets assume you have three Treepolicy1, Treepolicy2 and Treepolicy3 all "alive" in code in parallel, since you want to compare them. Here the chances are very high they share common parts you might want to refactor, for which unit tests are helpful. Moreover, those policies might be simple enough you can predetermine the output for a not overly complex input, which could make TDD feasible.

Doc Brown
  • 218,378