any document which says exactly what range of numbers are .NET BigIntegers designed for?

Question

I'm playing around with the .NET BigInteger and basically I'm wondering what number --an estimated answer would be fine-- is the point of deviation of the curve of (the graph of (increase of time required for operations) vs (value of BigInteger))?

or are they designed with no such deviation such that if we plot the increase of time required for operations vs value of BigInteger from 1 to infinity, we will have a smooth curve all the way?

for example, assuming arrays are designed with capability of handling 50 items . this means that if i have 1 item, operations are f(1) time. and when i have 2 items, operations are f(2) time. if i have 50 items, operations are f(50) time. but since it is designed for handling 50 items only, the operations done when we have 51 items will be g(51) where g(51) > f(51).

If implemented properly the complexity of BigInteger arithmetic should be a smooth curve. For example the time complexity of multiplication should be O(NM) where N is the number of digits in the first multiplicand, and M is the number of digits in the second multiplicand. Of course there are practical limits in that you could pick N and M so large that the numbers wouldn't fit in your machine.

Are there any / does anyone know of any documents claiming that it is implemented as such?

Answer 1

Any number that could possibly get larger than ULong.MaxValue, or smaller than Long.MinValue should be represented using BigInteger.

If NOT (Long.MinValue <= X <= ULong.MaxValue) Then BigInteger

BigInteger is for too large numbers than normal primitives can handle.

For example if your integer is outside the range of Long, you should probably use BigInteger. These cases are very rare though, and using these classes have significantly higher overhead than their primitive counterparts.

For example, long is 64 bits wide and can hold the range: -9,223,372,036,854,775,808 to 9,223,372,036,854,775,80. ulong can hold 0 to 18,446,744,073,709,551,615. If your numbers are larger or smaller than that, BigInteger is your only option

The only time I've seen them used in a real world application was a starchartting application.

See Also: Primitive Ranges in .NET

Answer 2

In some sense the point of BigInteger is not so much absolute size as it is unlimited precision. Floating point numbers can be very large too, but have limited precision. BigInteger lets you perform arithmetic with no concern about rounding errors or overflow. The price you pay is that it is hundreds of times slower than arithmetic with ordinary integers or floating point numbers.

As others have pointed out, ulong can hold between 0 to 18,446,744,073,709,551,615, and as long as you stay in that range you can do exact arithmetic. If you go even 1 beyond that range you'll get an overflow, so the answer to your question is use BigInteger if you need exact arithmetic and there is any possibility that any intermediate result will exceed 18,446,744,073,709,551,615.

Most problems in science, engineering and finance can live with the approximations forced by floating point numbers, and can't afford the time cost of BigInteger arithmetic. Most commercial calculations can't live with the approximations of floating point arithmetic, but work within the range 0 to 18,446,744,073,709,551,615, so they can use ordinary arithmetic. BigInteger is needed when using algorithms from number theory which includes things like cryptography (think 50 digit prime numbers). It is also sometimes used in commercial applications when exact calculations are needed, speed is not too important, and setting up a proper fixed decimal point system is too much trouble.

If implemented properly the complexity of BigInteger arithmetic should be a smooth curve. For example the time complexity of multiplication should be O(NM) where N is the number of digits in the first multiplicand, and M is the number of digits in the second multiplicand. Of course there are practical limits in that you could pick N and M so large that the numbers wouldn't fit in your machine.

If you google "Computational complexity of biginteger" you'll get more references than you can shake a stick at. One that speaks directly to your question is this: Comparison of two arbitrary precision arithmetic packages.

Answer 3

Memory Limit

BigInteger is relies on int array for storage. Assuming this, theoretical limit for maximum number, that BigInteger capable to represent, can be derived from maximum array size available in .net. There is a SO topic about arrays here: Finding how much memory I can allocate for an array in C#.

Assuming that we know maximum array size, we can estimate maximum number, which BigInteger can represent: (2^32)^max_array_size, where:

• 2^32 - maximum number in array cell (int)
• max_array_size - maximum allowed size of int array which is limited by object size of 2GB

This gives number with 600 millions of decimal digits.

Performance Limit

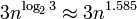As for performance, BigInteger uses Karatsuba algorithm for multiplication and linear algorithm for adding. Multiplication complexity is , that means it will scale pretty well even for large numbers (Complexity graph), however you can still can hit performance penalty depending on size of RAM and processor cache.

As far, as maximum number size is limited to 2GB, on descent machine you won't see unexpected performance gap, but still operating on 600 million digit numbers will be dead slow.

Answer 4

The limit is your memory size (and the time you have). So, you can have really big numbers. As said by Kevin, in cryptography one has to multiply or exponentiate numbers with some thousand (binary) digits, and this is possible without any problems.

Of course, often the algorithms get slower as the numbers get larger, but not so much slower.

When you are using numbers in the mega-digit range, you may want to think about other solutions, though - as really calculating with them gets slow, too.

Answer 5

There are a few uses within the scientific community (i.e. the distance between galaxies, number of atoms in a field of grass, etc..)

Answer 6

As kevin cline's answer suggests, BigNumbers were added to the .NET libraries primarlily because they were needed as a building block for many modern cryptographic algorithms (digital signatures, public/private key encryption, etc.). Many modern cryptographic algorithms involve calculations on integer values with sizes up to several thousand bits. Since the BigNumber class describes a well defined and useful class, they decided to make it public (rather than keeping it as an internal detail of the cryptographic APIs).