An exercise on decoders

Question

I have the following exercise:

Design a circuit that takes a 2 bit binary and makes it x^3 (x cubed), using a decoder 
of your choice.

I thought to do it with a 3 to 8 decoder, because I have 2 bits of input, and 4 bits of output, since the largest output is 11011 (which is 27 in decimal).

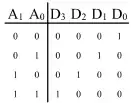
I have managed to get to a truth table. Input = \$x_0x_1x_2\$. Output= \$a,b,c,d,e\$.

\begin{array}{|c|c|c|c|c|c|c|c|} \hline x_0 & x_1 & x_2 & a & b & c & d & e \\ \hline 0 & 0 &0 &0 &0 &0 &0 &0\\ \hline 0 &0 &1 &0 &0 &0 &0 &1\\ \hline 0& 1 &0 &0 & 1 &0 &0 &0\\ \hline 0 &1 &1 &1 &1 &0 &1 &1\\ \hline \end{array}

However, I am not quite sure what should I do now. I have to get to a function to represent it in gates? How can I make a karnaugh map from that table?

I am aware that I would have to add three more outputs to the 3 to 8 decoder, but they will be just "don't cares".

Your help is appriciated.

Answer 1

With some thought you can do it with less logic ... a single 2-input gate.

I'll not give the whole game away, but one technique that may help is to treat each output bit individually, and minimise the logic for that output alone.

Start with bit c as it is the simplest.

Then put the individual solutions together.

Answer 2

To answer the question in general, from this point you would look at each output variable and construct the appropriate logic on that line.

Each of your output variables, in general, will be constructed independent of the others. However, there are often cases where there is similarity (or they are identical) and as such may be formed used into a single logic configuration and taken twice on the output. The following is taken directly from the wiki.

For instance, the truth table for a 2 to 4 decoder looks like this:

Where the output expressions are derived for each respective output variable with respect to the input states.

And from these expressions you can directly design the decoder: