My excercise is the following:
Make a circuit which outputs X^3 of two bit input of X.
Use the lowest number of HALF ADDERS as you can.
I don't really understand how to compute x cubed with half adders.
Any hints or help is appriciated.
My excercise is the following:
Make a circuit which outputs X^3 of two bit input of X.
Use the lowest number of HALF ADDERS as you can.
I don't really understand how to compute x cubed with half adders.
Any hints or help is appriciated.
Let the LSB of the number be \$a\$ and MSB be \$b\$. Then the number is \$2b+a\$ where, \$a,b\in\{0,1\}\$.
$$(2b+a)^3=8b^3 + 12ab^2+6a^2b+a^3$$
Since \$a,b\in\{0,1\}, \ a^3=a^2=a\$ , \$b^3=b^2=b\$ and \$a\times b = a\ AND\ b = ab\$.
$$\therefore (2b+a)^3=8b+18ab+a$$ $$=16ab+8b+2ab+a$$ $$=2^4\times ab+2^3\times b+2^2\times 0+2^1\times ab+2^0\times a$$
From this we can say that,
The 'carry out' of an half adder, with inputs \$a\$ and \$b\$, will be \$ab\$. So circuit can be implemented as given below.
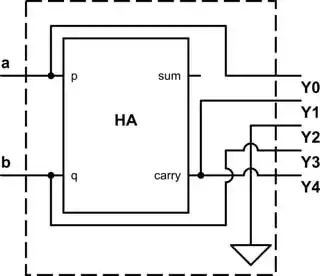
\$\mathtt{ba}\$ is the input and \$\mathtt{Y_4Y_3Y_2Y_1Y_0}\$ is the output (\$\mathtt{Y_0}\$ is the LSB).
The input of the circuit is a 2 bit number (max value = 3) and the hence the maximum value at output will be 27 (a 5 bit number). The truth table of the circuit is:
$$\begin{array}{cccccccl}&\mathbf{x} & &\mathbf{b} &\mathbf{a} & &\mathbf{Y_4} &\mathbf{Y_3} &\mathbf{Y_2} &\mathbf{Y_1} &\mathbf{Y_0} & &x^3\\ \hline &\style{color:red}{0} &\rightarrow &0 &0 & &0 &0 &0 &0 &0 &\rightarrow &\style{color:red}{0}\\ &\style{color:red}{1} &\rightarrow &0 &1 & &0 &0 &0 &0 &1 &\rightarrow &\style{color:red}{1}\\ &\style{color:red}{2} &\rightarrow &1 &0 & &0 &1 &0 &0 &0 &\rightarrow &\style{color:red}{8}\\ &\style{color:red}{3} &\rightarrow &1 &1 & &1 &1 &0 &1 &1 &\rightarrow &\style{color:red}{27}\\ \hline & & & & & &ab &b &0 &ab &a\\ \hline \end{array}$$
The 'carry out' of an half adder, with inputs a and b, will be \$ab\$. So circuit can be implemented as given below.

\$\mathtt{ba}\$ is the input and \$\mathtt{Y_4Y_3Y_2Y_1Y_0}\$ is the output (\$\mathtt{Y_0}\$ is the LSB).