Textbook's way of determining KVL polarities

Question

The following example is taken from Fundamentals of Electronics (4th ed.):

In the example there is a voltage source connected in series with two resistors. I've checked other questions [Ref] [Ref] and as I understand it, the polarity of the resistors can be chosen, as long as it is done consistently: the polarity is "the sign (direction) of the current". However, I'm still a little baffled by the above example.

The way the authors have labelled it I expected the polarity of V2 to have been reversed. This would match other examples I have seen [Ref].

So, what am I missing? How can V1 and V2 have opposing polarities?

Answer 1

Actually, it does not matter. It is kind of an arbitrary assumption. You just make a assumption about polarity. If the result is negative, then just change your decision to the opposite.

Let choose arbitrary polarities (V1 and V2) and a closed KVL loop:

1st KVL equation: $$20V - I.R_2 - I.R_1 = 0$$ And We know that: $$V = I.R$$ $$20V = I.(2+3)\Omega$$ $$ I = 4A$$ so $$V_1 = 8V, \quad V_2 = 12V$$

For same direction loop but V2 reversed:

2nd KVL: $$20V - I.R_2 + I.R_1 = 0$$ Current is still 4A. These time $$V_1 = 8, \quad V_2 = -12V$$

As you can see quantity of voltage does not change. Minus result means you decided wrong polarity of voltage but there is nothing to worry about. Just change the polarity opposite direction.

Answer 2

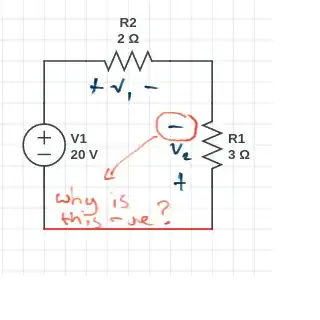
Looks like by polarities they mean the current direction in a circuit branch.

Instead of looking at elements, if you can assume a current direction for each branch, the polarities for elements will follow naturally.

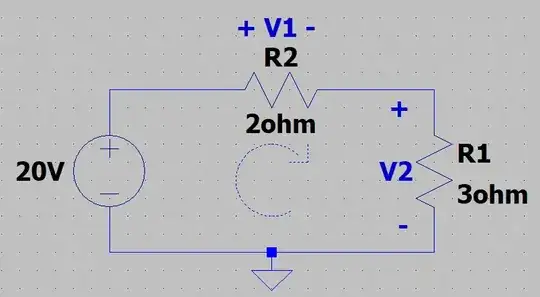
After choosing an arbitrary current direction for each branch, separately, designate circuit loops (in this case a single loop).

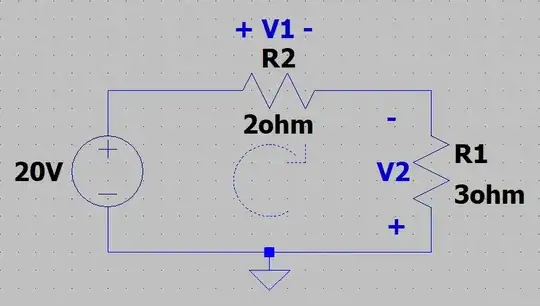
In the example above, if you choose a clockwise current direction in the branch (the whole circuit is a single branch), and separately designate the loop as counter clockwise (in this case the branch is also the whole loop, but usually a loop would trace across several branches):

-20V + I.R_2 + I.R_1 = 0

(Starting from just above the 20 V source, and going counter clockwise, you're moving against the designated current flow direction & therefore should add the I*R elements).

After solving the equation, the current will end up positive, indicating that the arbitrarily chosen clockwise direction (for current flow) was correct.

Since the chosen branch direction is clockwise, all the resistor polarities are clockwise as well. (I don't think it's allowed to choose two different polarities for resistors on the same branch).

(Moving around the loop counter clockwise was not the intuitive direction, but had been chosen to show that the procedure works regardless of how you trace the circuit loop).

So the two things you're allowed to choose are:

1. The current flow direction for each branch (this will also designate the polarity of all the elements at each branch).
2. The direction at which you trace your KVL loop
3. (If the KVL loop trace path matches the designated current flow direction in a particular branch, you'd subtract the voltage drop across resistors in that branch when writing KVL. Whereas if the loop advancement across a branch is in the opposite direction to the designated flow direction in that branch, you'd be adding the resulting voltage across resistors, rather than substructing it). (The "resulting" voltage across resistors is I * R in absolute value).

Answer 3

While @anilberg's answer is spot on, I want to give another example that is more physical in nature to help lock it in. Let's take a standard voltmeter or, in today's era, a Digital Multimeter (or DMM) and examine the circuit with it.

It has a red lead connected to the positive voltage terminal and a black lead for the negative or common terminal. That is important for how the meter will read. Where you choose to denote the positive and negative sides of a component like a resistor for the KVL equations corresponds to how the DMM would read if attached to the circuit. And, just like you could buy a DMM for each component and hook one up in either direction (red/black or black/red) on each resistor, capacitor, inductor, or other two-terminal component, you can do the same when writing out the KVL polarities and equations. However, that direction will correspond to the sign you need to use when writing an equation for each loop/branch. If you swap the direction of the polarity, then the final answer for that voltage will have it's sign flipped. However, it still holds the same meaning. A negative voltage with the plus sign written on the bottom of the component means the same thing as seeing a positive voltage in the answer if you wrote it with the plus sign on the top of the component.

It's just like how in this picture, they are reading a negative voltage on the battery because they used the negative/black lead of the DMM on the positive/plus side of the AA battery they are measuring:

Answer 4

Assume positive and negative polarities across a element in any direction. Usually current flows form positive to negative polarities and current flowing from positive to negative is assumed positive. If you get negative current, then the polarity you assumed was opposite. This is true even in case of voltage and current sources. Look at Passive sign convention.