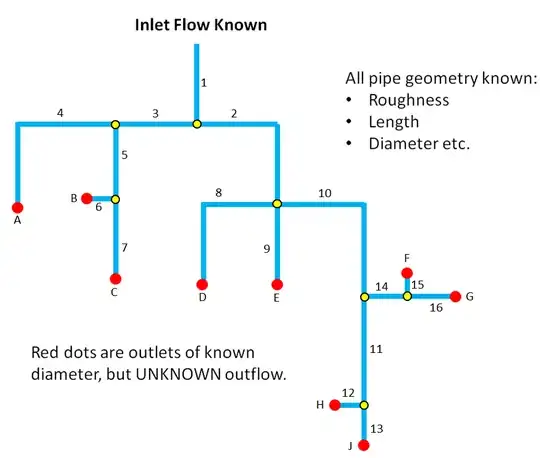
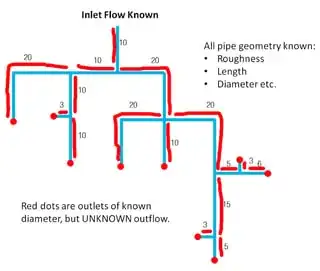
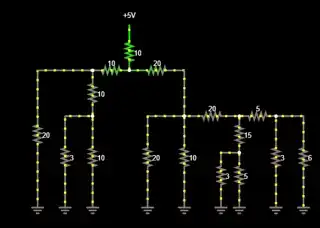
I have little/no experience with pipe networks and have been searching for a methodology to calculate the discharge from multiple outlets of an oil pipe network with a single inlet. As far as i can tell I have too many unknowns to use something like the Hardy Cross method (and often i don't have loops, just multiple branches and outlets as shown below), and Hardy-Cross seems to be used to find flows in pipes with known inflows and outflows, which I don't have.
A good example may be something like this:
- Inlet flow rate is known
- Fluid Properties are known
- Geometry of all pipes/bends/outlets are known
- The height above a datum of all pipes and outlets are known
- Flow is each pipe branch is UNKNOWN
- Discharge from each outlet is UNKNOWN (ext. pressure can be assumed ambient)
- I have target outflows, and could modify pipe length/diameters to obtain them
Can anybody suggest an analytical method I can use to calculate the outflows and/or optimise the pipe lengths to obtain a set of target outflows?
A worked example of a similar problem would also be appreciated.
The person who tried to solve this problem before me just divided the inflow up based on the area of the outlets, without considering losses, bends or even the lengths of the pipes anywhere in the network. I have been searching for a while with limited resources for a worked example or solution method for this.
I will probably write a code to solve these problems if I find an appropriate methodology. (I'm aware commercial software does exist that could calculate this, but I don't have access).