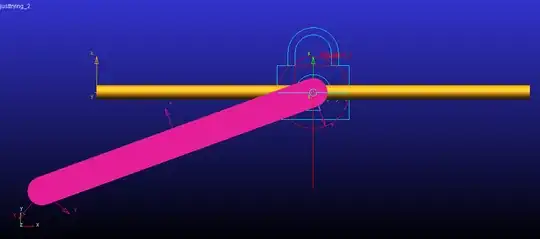
I'm trying to use ANSYS to solve statically a dynamic problem. As shown in the image below, there is an orange bar that is constraint to slide horizontally only and attached to another bar (pink) through a pin joint. When the orange bar is subjected to a momentary external force, it accelerates horizontally and as a result the pink bar behaves as a pendulum.
I modeled the case in ADAMS to get all the needed kinematics/dynamics info (accelerations, pin joint reactions, angle Vs time and etc.) and now would like to use ANSYS in order to obtain the stress and deflection fields. I am familiar with the flex body option in ADAMS and actually experienced with it a little, but would like to analyze the stress with a tool I feel more comfortable with.
As long as I understand, in cases by which the rigid body is actually moving - there is an option called Inertia relief. The general idea behind it is to "remove" the loads causing a motion in order to solve a static problem and compute the stress acting on the body. In this case, if I use a pin joint in ANSYS and apply horizontal acceleration on the pink bar - the all body would move. Alternatively, I can fix the bar to the pin joint in all 6 DOF but then I'll get an artificial and non-realistic bending moment (this moment generates the motion and does not bend the bar in reality). However, when using this Inertia relief option, all the support reactions are zeroed - and this should not be the case here. I need to fix the motion in X and Y directions in the pin joint while allowing the bar to rotate along the Z axis and solve the problem statically. I think to not use the Inertia relief option and alternately add linear acceleration (D'alembert style) but I'm not sure about it. Any ideas or thought?