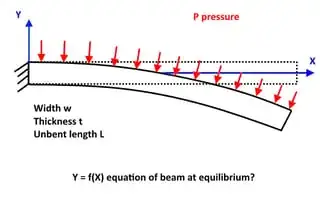
I have a strip of stainless steel encastree'd at one end to which is applied a constant pressure on one side, and I need to know what the deflection equation y = f(x) is at equilibrium. If the deflection was small I would be able to use one of the very well known deflection formulas which assume vertical loads, but it isn't.
I am trying to work out the bending moment M=f(x) using integrals to use: $$y(x)=\int\int_{beam} \frac{M}{EI}dx^2$$ But I'm getting more and more confused. What is the right approach to solving this problem?
Here is a diagram: