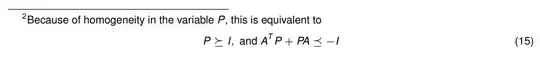I am currently learning about using Lyaponuv functions to find Linear Matrix Inequalities (LMIs) as conditions for stability of a linear time invariant system.
i.e. $$ \dot{x}(t) = Ax(t) $$ is stable if there exists a function $V(x)$ such that $V(x)>0$ for all $x \neq 0$ and $V(0) = 0$ and $\dot{V}(x) < 0$ for all $x \neq 0$
Generally we have learned to do this with a quadratic Lyapunov function $V(x) = x^TPx$ where $P\succ 0$ and $A^TP + PA \prec 0 $, but I just came across this footnote which I am struggling to understand.
The $P$ matrix also has to be symmetric which I am not sure why is true.
When performing convex optimisation on systems with Lyaponuv functions our lectures sometimes use the first LMIs i.e. $P \succ 0$ and other times we use $P \succeq I $ and I am not sure when and why the difference arises.