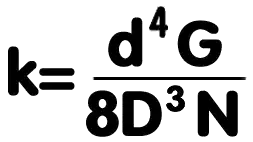The values that you have provided don't make too much sense, as you might have already noted in the comments below your question. But I am going to assume you are just doing as example, so the values are not the actual ones but just hypothetical.
Besides, the stiffness of the spring (longitudinal or torsional) changes with the amount of load; i.e. the stiffness is not constant. Say, if the spring deflects 1 mm for a load of 1000 N, or rotates 1 deg for a torque of 1000 N.mm, then it won't be 2 mm for 2000 N or 2 deg for 2000 N.mm. This implies that the stiffness is not constant, infact for any practically possible structure present in the world. You can only use that formula for extremely small deflections (for longitudinal spring) and rotations (for torsional spring).
Furthermore, the number of turns is an input and not an output, so it needs to be inputted if you want to figure out the spring's stiffness. Number of turns are usually decided when we need to achieve a certain level of stiffness for the spring. It can be anything, 4 or 8 or 40 or 120 etc.
So what you can do is that you can decide on the amount of longitudinal deformation you want (if the spring is longitudinal), like say you only want it to deform to 222 mm from 220 mm for this loading condition. Then divide this load by by 2 mm (i.e. 222 - 220), and that is the linear stiffness for the spring (again note that it might not be the same if the load changes since stiffness is non-linear in reality). Use this stiffness value in the equation you have already posted in your question, and then find out the number of turns required on the spring, that will give you a deformation of 2 mm.