Hi I read this response but it isn't exactly my situation I have a circle where the axis of rotation is on the c axis like this for a segment equal to the green.
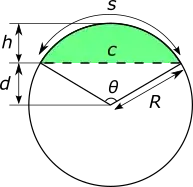
Specifically, I have a round steel plate on a concrete base attached with anchors. There a moment across the center (out of plane) I am trying to determine the resisting moment of the concrete surface.
I am very much not sure what the integration result would be.
I think I found my answer, thanks to https://structx.com/Shape_Formulas_003.html and the Parallel axis theorem https://en.wikipedia.org/wiki/Second_moment_of_area.
$I_x$ around the center of the circle is
$I_x=\frac{r^4}{8}(\theta-\sin{\theta}+2\sin{\theta}\sin^2{\frac{\theta}{2}})$
From the Theorem
$I_{x'}=I_x-Ad^2$
Where $d$ is the distance between the center of the circle and the line
$A$ is the area $A=\frac{r^2}{2}(\theta-\sin{\theta})$
The formula you can use is:
$$I=\frac{1}{8}R^4(\theta- sin\theta cos\theta) $$
Where:
I is the second area moment of the circular segment about the chord.
R is the radius of the circle.
θ is the angle (in radians) subtended by the circular segment at the center of the circle.
Maximum stress to the concrete happens at the top of the segment H=R and is
$$\sigma=\frac{M*C}{I}$$
