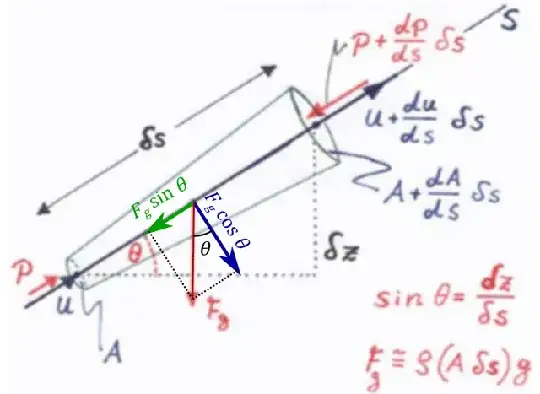
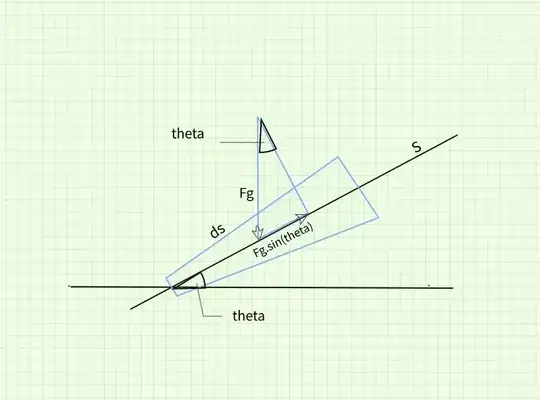
As far as I can understand the sum of the applied forces is the component of the weight of the fluid in the s direction and pressure forces. Looking at the diagram it seems the component of Fg is Fg/sin(θ). Because,
sin(θ) = Opposite side / Hypotenuse
sin(θ) = Fg / Fgs
Fgs = Fg / sin(θ)
(Fgs is the component of Fg along the s direction)
But my lecture notes says the component is Fg sin(θ).
For more context, the note is regarding the derivation of the Bernoulli equation.
Since $\sin(\theta)\in [-1, 1]$, that would mean $\left|F_g/\sin(\theta)\right|\ge F_g$. So $F_g$ would produce greater force than itself in the $s$ direction and as the angle $\theta$ approaches 0, this force would go to $\infty$.
So I would say the derivation in the textbook is actually correct. You can always replace a vector, in this case $F_g$ by a sum of other vectors: $$\overrightarrow{F}_g = \sum \overrightarrow{F}_{g,i}$$
If a direction is given by an angle $\theta$ in 2D, then a component in this direction is $F_g\cdot \cos(\theta)$ and perpendicular component to that directio is $F_g\cdot \sin(\theta)$.
You differential element is At an angle $\theta \ $with respect to x axis but the weight vector is pointing down. .
You can think of $F_g.sin \theta$ as the inclined component of the weight of the differential element laying on a frictionless ramp with an angle $\theta$.
This component is zero if the $\theta=0 \ $and is one when $theta = 90\ $ and varies as $ F_g.sin\theta \ .$
All the other forces are along $\theta \ $
Refer to the diagram please.
.
