I'd like to compute the response to a step function of a electrical/thermal system. Generally I can "easily" compute the transfer function $H$:
$$H(\omega) = \frac{V_{out}(\omega)}{V_{in}(\omega)}$$
Since the Fourier transform ($\mathcal{F}$) of the Heaviside function is (computed with WA):
$$\mathcal{F}(\theta(t)) = V_{in}(\omega) = \sqrt{\frac{\pi}{2}}\delta(\omega)+\frac{i}{\sqrt{2\pi}\omega}$$
Hence, noting $\mathcal{IF}$ the Inverse Fourier transform:
$$V_{out}(t) = \mathcal{IF} \left\{ \left( \sqrt{\frac{\pi}{2}}\delta(\omega)+\frac{i}{\sqrt{2\pi}\omega} \right) H(\omega) \right\}$$
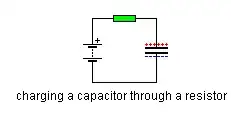
To check my math I tried to compute the response for a simple RC system:
I should get the well known charge of the capacitor. The transfer function:
$$H(\omega) = \frac{1}{1+i\omega R C}$$
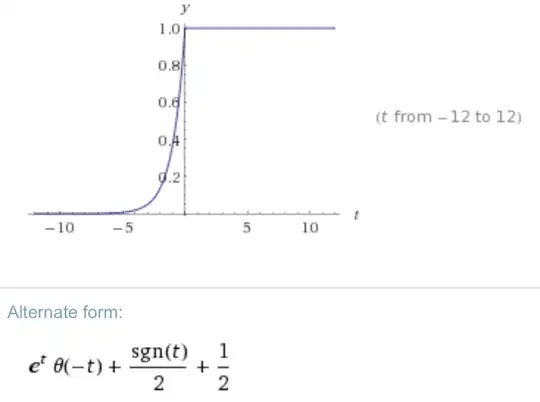
Computing the Inverse Fourier transform ($\mathcal{IF}$) with WA ($R=C=1$) I get:
This would be correct if we were going backward in time :/. So the question is... What am I doing wrong?
I did the same using Laplace Transforms and everything works fine... But I don't understand why.
P.S. I don't want another method, I just want to understand what's wrong in my approach.
P.S. the reason why I am using WA is that for my more complicated system I need to compute the Fourier transforms using WA.