I've been designing an electric skateboard which is driven by only one of the rear wheels (for the moment). As I was picking out motors for the board, I soon realized I would need to find a balance between torque needed to climb hills, and RPM to get a good top speed.
So I'm searching for the best KV (RPM/v) motor/gearing ratio combination.
For all calculations I've assumed the following:
- Total mass (board + rider) = 85 kg
- Voltage = 12 Cells * 3.2V (LiFePo4) = 38.4 V
- Max Speed = 40 km/h = 11.11 m/s
- Hill Grade = 15%
- Coefficient of friction between rubber and asphalt: 0.65
- Diameter of wheel = 80 mm
I tried assuming maximum kinetic energy as being equal to maximum gravitational potential energy at the top of the hill.
$$E_{k,max} = \frac{1}{2}mv_{max}^2 = E_g = mgh_{max}$$
Then solving for $h$.
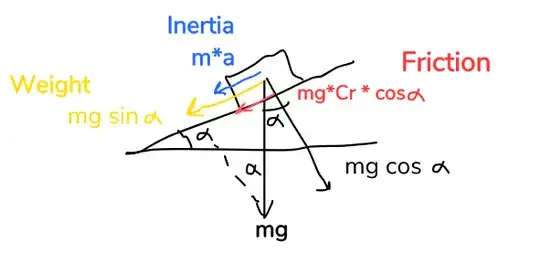
I'd take that and use $y/x = 0.2$, solve for $x$, then use some trigonometry to setup a Newton's Second Law problem and solve for force needed to overcome friction and gravity (Equilibrium problem).
Then using $T = F \times r$, find torque needed at the wheels, assume some gearing ratio that keeps that and the $V_{max}$. Then solve for RPM and divide by total voltage for motor KV.
My mechanics are rather rusty and I could use some help.