In a simple situation, one simply takes the average of outer diameter and inner diameter to gain the mean radius for calculating torque transmission through a contact face, such as a clutch.
But how would you work this out if there was no simple ID and OD to work with, say for example if the ID was broken by an array of holes as shown below:
In a clutch, the torque transmitted can be calculated by integrating the torque contribution of the shear pressure over the contact area.
$$\tau=\int \sigma\,r \; dA$$
The shear pressure will be equal to the friction coefficient multiplied by the contact pressure:
$$\sigma=\mu\,p$$ $$\tau=\int \mu\,p\,r \; dA$$
usually the contact pressure is considered constant, as areas of higher pressure tend to wear faster, reducing the pressure. Coefficient of friction is also usually considered constant. Thus those can be brought outside the integral:
$$\tau=\mu\,p \int r \; dA$$ $$\tau=\mu\,\frac{F}{A} \int r \; dA$$ $$\tau=\mu\,F\frac{\int r \; dA}{A} $$ So it's this mean radius that indeed you care about: $$\frac{\int r \; dA}{A} $$ For a solid circle this gives: $$\frac{\iint r\,d\theta\,dr}{\iint 1\,d\theta\,dr}$$ $$\frac{\int 2\,\pi\,r^2\,dr}{\int 2\,\pi\,r\,dr}$$ $$\frac{\frac23 \pi\,r^3}{\pi\,r^2}$$ $$\frac23 r$$
If you have a ring with outside radius $R_2$ and inside radius $R_1$ then you can just subtract the integrals on top and bottom: $$\frac{\iint r\,d\theta\,dr_2 - \iint r\,d\theta\,dr_1}{\iint 1\,d\theta\,dr-\iint 1\,d\theta\,dr_1}$$ $$\frac{\frac23 \,\pi\, {r_2}^3 - \frac23 \,\pi\, {r_1}^3}{\pi\, {r_2}^2 - \pi\, {r_1}^2}$$
$$\frac23\left(r_1+r_2-\frac{r_1\,r_2}{r_1+r_2}\right)$$
This is close to the commonly sighted approximation $\frac{r_1+r_2}2$:
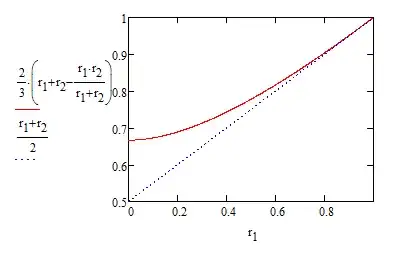
This graph assumes an outside radius of 1 and plots the mean effective radius varying the inner radius. It shows that the approximation is close when the mean radius is more than about half the size of the outer radius.
If you'd like to account for holes in your clutch plate you can use a similar method to the above. However, given most people just use the mean of the radii approximation, I don't think the added accuracy is likely necessary.
