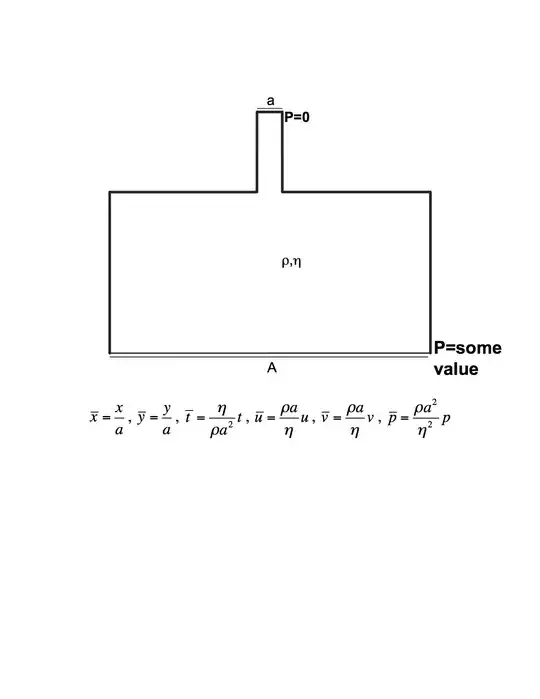
I have been working with an old code for modeling incompressible, 2D viscous flow out of a tank to understand a chemical process. There isn't much documentation and I'm not a fluid dynamicist, so I have been trying to check that things are working as they should by comparing results with those from another code. The comparison is great when I use a velocity inlet condition. However, there is a major discrepancy when I use a pressure inlet condition. In both cases, the outlet pressure is zero.
I have spent several weeks trying to figure out what the problem is with the pressure inlet condition (and have an active question about it) because I have pressure inlet values that I want to use in my problem. I don't know velocity inlet values. But I have to acknowledge I've hit a wall with figuring out my pressure inlet boundary condition problem.
This may be a dumb question, but I would really appreciate it if someone would help me confirm if I can transform my pressure values into an inlet velocity condition. If I can, maybe I can simply use an inlet velocity and my problems will be over!
I understand that: $$P = \dfrac{1}{2}\rho U^2 + \rho gz$$
where $\rho$ is fluid density, $U$ is velocity, $g$ is the acceleration of gravity, and $z$ is depth of the tank inlet below the tank outlet at 0.
So if I simply plug in my inlet pressure value and rearrange, will I get a valid inlet velocity that I can use for a velocity boundary condition? My concern is that I'm dealing with viscous flow and I think this expression is related to the Bernoulli equation, which does not account for viscous flow.
If I'm right and I can't use this expression to calculate an inlet velocity, does anyone know if there's an alternative?
The reason I say I probably can't is that I've tried it and the results from the two codes don't match. I'm just trying to figure out where my problem is--if it's likely to be a bug in one of the codes, which code is the problem, or if I'm making some mistake when inputting my boundary condition values.